|
7. RECHERCHE DU FLOT MAXIMUM |
| DEFINITIONS |
| Réseau de transport |
Un réseau de transport est un graphe sans boucle, où chaque arc
est associé à un nombre c(u) ![]() 0, appelé "capacité" de l'arc u. En
outre, un tel réseau vérifie les hypothèses suivantes.
0, appelé "capacité" de l'arc u. En
outre, un tel réseau vérifie les hypothèses suivantes.
Il existe un seul noeud s qui n'a pas de prédécesseurs, tous les autres en ont au moins un. Ce noeud est appelé l'entrée du réseau, ou la source.
Il existe également un seul noeud p qui n'a pas de successeurs, tous les autres en ont au moins un. Ce noeud est appelé la sortie du réseau, ou le puits.
| Flot |
Un flot f dans un réseau de transport est une fonction qui associe à chaque arc u une quantité f(u) qui représente la quantité de flot qui passe par cet arc, en provenance de la source et en destination du puits.
Un flot doit respecter la règle suivante: la somme des quantités de flot sur les arcs entrants dans un noeud (autre que s et p) doit être égale à la somme des quantités de flot sur les arcs sortants de ce même noeud. En d'autres termes, la quantité totale de flot qui entre dans un noeud est égale à la quantité totale de flot qui en sort.
| Flot compatible |
Un flot f est compatible avec un réseau si pour tout arc
u, 0 ![]() f(u)
f(u) ![]() c(u). Autrement dit, pour chaque arc, le flot qui le
traverse ne doit pas dépasser la capacité de l'arc.
c(u). Autrement dit, pour chaque arc, le flot qui le
traverse ne doit pas dépasser la capacité de l'arc.
| Flot complet |
Un flot f est complet si pour tout chemin allant de la source au puits, il y a au moins un arc saturé, i.e. le flot qui le traverse est égal à la capacité de l'arc.
| PROBLEME DU FLOT MAXIMUM |
Connaissant les capacités des arcs d'un réseau de transport, le problème du flot maximum consiste à trouver quelle est la quantité maximum de flot qui peut circuler de la source au puits. L'algorithme le plus connu pour résoudre ce problème est celui de Ford et Fulkerson. Nous verrons deux approches pour cette méthode. La première est basée sur la recherche d'une chaîne dans le réseau alors que la seconde construit un graphe "d'écart" dans lequel on recherche un chemin.
| ALGORITHME DE FORD-FULKERSON, CHAINE AUGMENTANTE |
On part d'un flot compatible. Le plus évident est le flot nul, i.e. pour tout arc u, f(u) = 0. Ensuite, on cherche une chaîne reliant la source au puits telle que son flot peut être augmenté. Si on n'en trouve pas, le problème est résolu. Sinon, on augmente le flot sur cette chaîne. Ensuite, on recommence à chercher une chaîne augmentante et ainsi de suite. Une chaîne augmentante, i.e. une chaîne pour laquelle le flot peut être augmenté est une chaîne pour laquelle les arcs dans le sens direct n'ont pas atteint leur limite maximum et les arcs en sens indirect ont un flot non nul qui les traverse. L'augmentation de flot maximum pour une chaîne est le minimum des écarts entre le flot courant et le flot maximal pour les arcs directs ou le flot courant pour les arcs indirects. Autrement dit, une chaîne C est augmentante si:
pour tout arc u direct, f(u) < c(u),
pour tout arc u indirect, f(u) > 0.
Le flot sur cette chaîne C peut être augmenté de:
min({c(u) - f(u) | u
C et u sens direct}
{f(u) | u
C et u sens indirect})
| Exemple |
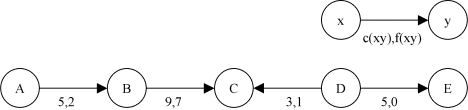
Voici une chaîne augmentante de A à E faisant partie d'un réseau de transport.
Dans cette chaîne, on peut augmenter le flot de:
3 entre A et B,
2 entre B et C,
1 entre C et D,
5 entre D et E.
On augmentera donc de 1 le flot dans cette chaîne. Ce qui signifie:
augmenter de 1 le flot entre A et B,
augmenter de 1 le flot entre B et C,
diminuer de 1 le flot entre D et C,
augmenter de 1 le flot entre D et E.
On remarque que pour les arcs en sens inverse, augmenter le flot signifie réduire le flot dans le sens direct. Entre D et C, le flot est réduit de 1 pour permettre l'arrivée d'une unité de flot sur C par B tout en conservant l'équilibre du noeud. D ayant une unité de trop, son équilibre n'est pas respecté. C'est pourquoi une unité de flot supplémentaire circule entre D et E.
| Algorithme principal |
Titre: FordFulkerson1
Entrées: R = (X;U;c) un réseau, s et
p deux sommets.
Sorties: f() une fonction indiquant le flot circulant à travers chaque
arc.
Variables intermédiaires: C un sous-ensemble d'arcs, u un
arc, m et a deux réels.
Début
pour tout arc u Fin ![]() U faire f(u)
U faire f(u) ![]() 0;
0;
tant que ![]() une chaîne C augmentante entre s et p
une chaîne C augmentante entre s et p ![]() R faire
R faire
m ![]() +oo;
+oo;
pour tout u ![]() C faire
C faire
si u en sens direct alors a ![]() c(u)
- f(u) sinon a
c(u)
- f(u) sinon a ![]() f(u);
f(u);
si a < m alors m ![]() a;
a;
fin pour;
pour tout u ![]() C faire
C faire
si u en sens direct alors f(u) ![]() f(u)
+ m sinon f(u)
f(u)
+ m sinon f(u) ![]() f(u) - m;
f(u) - m;
fin pour;
fin tant que;
| Algorithme de recherche d'une chaîne augmentante |
L'idée est la même que pour la recherche d'un chemin (cf. méthode avec le graphe d'écart). On parcours le réseau jusqu'à visiter le noeud p. Cependant, on utilisera un arc pour se déplacer:
s'il est direct et qu'il n'a pas atteint son flot maximum,
ou s'il est indirect et qu'il n'a pas un flot nul.
| Algorithme |
Titre: RechercherChaineAugmentante
Entrées: R = (X;U;c) un réseau, s et
p deux sommets, f() le flot courant.
Sorties: pred() une fonction indiquant par quel arc on arrive à un noeud
donné à partir de s.
Variables intermédiaires: X' un sous-ensemble de noeuds,
accessible() une fonction qui indique si un noeud est accessible à partir de
s, x et y deux noeuds.
Début
X' ![]() {s};
{s};
pour tout x ![]() X faire
X faire
accessible(x) ![]() faux;
faux;
pred(x) ![]() nil;
nil;
fin pour;
marqué(s) ![]() vrai;
vrai;
tant que X' ![]()
![]() et non accessible(p) faire
et non accessible(p) faire
choisir x ![]() X';
X';
X' ![]() X' - {x};
X' - {x};
pour tout u = (x;y) ![]() U faire
U faire
si non accessible(y) et f(u) < c(u) alors
X' ![]() X'
X' ![]() {y};
{y};
pred(y) ![]() x;
x;
accessible(y) ![]() vrai;
vrai;
fin si;
fin pour;
pour tout u = (y;x) ![]() U faire
U faire
si non accessible(y) et f(u) > 0 alors
X' ![]() X'
X' ![]() {y};
{y};
pred(y) ![]() x;
x;
accessible(y) ![]() vrai;
vrai;
fin si;
fin tant que;
Fin
| ALGORITHME DE FORD-FULKERSON, GRAPHE D'ECART |
Comme pour la méthode précédente, on part d'un flot compatible. Ensuite, on construit un graphe d'écart à partir de ce flot. Ce graphe d'écart représente les modifications de flot possibles sur chaque arc. Sur ce graphe, les noeuds ont exactement la même signification que dans le réseau de transport. Par contre, un arc indiquera de combien il est possible d'augmenter le flot entre deux noeuds. Ainsi, pour un arc u = (x;y), on créera dans le graphe d'écart:
un arc de x à y de capacité c'((x;y)) = c(u) - f(u) si c(u)
 f(u),
f(u), un arc de y à x de capacité c'((y;x)) = f(u) si f(u)
 0.
0.
Ensuite, dans ce graphe d'écart, on cherchera un chemin de la source au puits. Si on n'en trouve pas, le problème est résolu. Sinon, on augmente le flot sur ce chemin, qui correspond en fait à une chaîne si l'on se ramène à la première méthode. Le flot sera augmenté de la plus petite capacité des arcs du chemin. Autrement dit, le chemin C sera augmenté de:
min{c'(u) | u
C}
| Exemple |
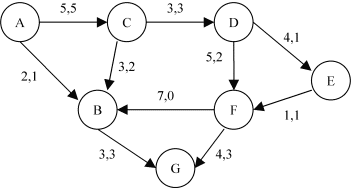
Voici un réseau transport dans lequel circule un flot.
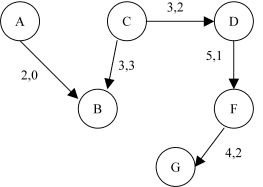
Le graphe d'écart correspondant est le suivant.
(A,B,C,D,F,G) est un chemin pour aller de A à G. On peut augmenter le flot de:
2 entre A et B,
3 entre B et C,
1 entre C et D,
4 entre D et F,
2 entre F et G.
On augmentera donc le flot de 1 sur ce chemin, ce qui signifie:
augmenter de 1 entre A et B,
réduire de 1 entre C et B,
augmenter de 1 entre C et D,
augmenter de 1 entre D et F,
augmenter de 1 entre F et G.
On remarque que le chemin (A,B,C,D,F,G) trouvé correspondait à la chaîne augmentante (A,B,C,D,F,G).
| Algorithme principal |
Titre: FordFulkerson2
Entrées: R = (X;U;c) un réseau, s et
p deux sommets.
Sorties: f() une fonction indiquant le flot circulant à travers chaque
arc.
Variables intermédiaires: G = (X;U') un graphe,
c'() une fonction indiquant la capacité d'un arc de G,
Début
pour tout arc u ![]() U faire f(u)
U faire f(u) ![]() 0;
0;
construire le graphe d'écart G;
tant que ![]() un chemin C entre s et p
un chemin C entre s et p ![]() G faire
G faire
m ![]() +oo;
+oo;
pour tout u ![]() C faire si c'(u) < m alors m
C faire si c'(u) < m alors m ![]() c'(u);
c'(u);
pour tout u ![]() C faire
C faire
si a(u) est direct alors f(a(u)) ![]() f(a(u)) + m;
f(a(u)) + m;
sinon f(a(u)) ![]() f(a(u)) - m;
f(a(u)) - m;
fin pour;
construire le graphe d'écart G;
fin tant que;
Fin
| Construction du graphe d'écart |
Pour construire le graphe d'écart G, il suffit de parcourir tous les arcs du réseau R et de créer pour chacun un ou deux arcs dans G selon la méthode expliquée précédemment.
| Algorithme |
Titre: ConstruireGrapheEcart
Entrées: R = (X;U;c) un réseau, f() le
flot courant sur R.
Sorties: G = (X;U') le graphe d'écart, c'() une
fonction indiquant la capacité d'un arc de G, a() une fonction
indiquant à quel arc de R correspond un arc de G.
Variables intermédiaires: u un arc, x et y
deux noeuds, m un réel.
Début
pour tout u = (x;y) ![]() U faire
U faire
si f(u) > 0 alors
U' ![]() U'
U' ![]() {(y;x)};
{(y;x)};
c'((y;x)) ![]() f(u);
f(u);
a((y;x)) ![]() u;
u;
fin si;
si f(u) < c(u) alors
U' ![]() U'
U' ![]() {(x;y)};
{(x;y)};
c'((x;y)) ![]() c(u) - f(u);
c(u) - f(u);
a((x;y)) ![]() u;
u;
fin si;
fin pour;
Fin
| Recherche d'un chemin |
Pour rechercher un chemin entre s et p, il suffit de parcourir le graphe dans le sens des arcs et de marquer les noeuds que l'on visite. On ne visitera pas deux fois un même noeud. Pour effectuer ce parcours, on dispose d'un ensemble X' des noeuds restant à visiter. Au départ il n'y a que s. Ensuite, à chaque itération, on prend un noeud dans X', on le marque pour éviter de le visiter à nouveau, on l'enlève de X' et on met ses successeurs dans X', seulement s'ils ne sont pas déjà marqués. On s'arrête quand on a visité p.
| Algorithme |
Titre: RechercherChemin
Entrées: R = (X;U;c) un réseau, s et
p deux sommets, f() le flot courant.
Sorties: pred() une fonction indiquant par quel arc on arrive à un noeud
donné à partir de s.
Variables intermédiaires: X' un sous-ensemble de noeuds,
accessible() une fonction qui indique si un noeud est accessible à partir de
s.
Début
X' ![]() {s};
{s};
pour tout x ![]() X faire
X faire
accessible(x) ![]() faux;
faux;
pred(x) ![]() nil;
nil;
fin pour;
accessible(s) ![]() vrai;
vrai;
tant que X' ![]()
![]() et non accessible(p) faire
et non accessible(p) faire
choisir x ![]() X';
X';
X' ![]() X' - {x};
X' - {x};
pour tout u = (x;y) ![]() U faire
U faire
si non accessible(y) alors
X' ![]() X'
X' ![]() {y};
{y};
pred(y) ![]() x;
x;
accessible(y) ![]() vrai;
vrai;
fin si;
fin pour;
fin tant que;
Fin
|