|
2. LES ARBRES |
| DEFINITIONS ET THEOREMES |
| Nombre d'arcs dans un graphe |
Soit n le nombre de noeuds d'un graphe
G = (X;U), n = |X|.
Soit m le nombre d'arcs de G, m = |U|.
Si G est connexe, m ![]() n - 1.
n - 1.
Si G est sans cycle, m ![]() n - 1.
n - 1.
| Arbre |
Un arbre est un graphe connexe sans cycle. Il a donc n - 1 arcs. On peut donc dire qu'un arbre est un graphe qui connecte tous les noeuds entre eux avec un minimum d'arcs.
| Remarques |
L'ajout du moindre arc supplémentaire dans un arbre crée un cycle.
Un graphe connexe possède un graphe partiel qui est un arbre.
| Exemple |
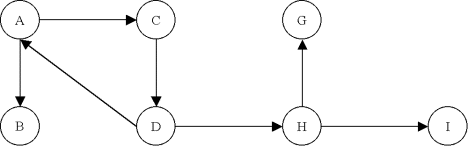
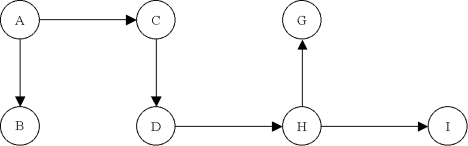
Un graphe connexe:
Un arbre extrait du graphe précédent:
| Forêt |
On appelle forêt un graphe dont chaque composante connexe est un arbre.
| Racine, antiracine |
Un noeud a d'un graphe G est une racine de G s'il existe un chemin joignant a à chaque noeud du graphe G.
Un noeud a d'un graphe G est une antiracine de G s'il existe un chemin joignant chaque noeud du graphe G à a.
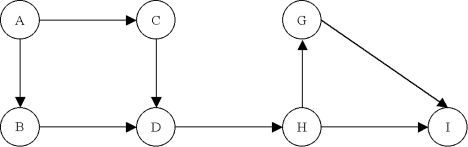
| Exemple |
A est une racine du graphe.
I est une antiracine du graphe.
| Arborescence, anti-arborescence |
Un graphe G est une arborescence de racine a si G est un arbre et si a est une racine.
Un graphe G est une anti-arborescence d'antiracine a si G est un arbre et si a est une antiracine.
| ARBRE DE COUT MINIMUM / MAXIMUM |
Imaginons que l'on associe une valeur, un poids, à chaque arc d'un graphe G. Le problème de l'arbre de coût maximum consiste à trouver un arbre, graphe partiel de G, dont la somme des poids des arcs est maximum. En pratique, les problèmes se ramène plutôt à trouver l'arbre de coût minimum, ce qui ne change pas fondamentalement le principe des algorithmes proposés ici.
Par exemple, minimiser le coût d'installation de lignes électriques entre des maisons peut être modélisé par la recherche d'un arbre de coût minimum. En effet, on veut connecter toutes les maisons entres elles sans avoir de lignes inutiles (d'où la recherche d'un arbre). Ensuite, on veut utiliser le moins de câble possible, aussi on associera à chaque possibilité de connexion la longueur de câble nécessaire et on cherchera à minimiser la longueur totale de câble utilisée.
Dans ce cours, deux algorithmes sont proposés. L'efficacité de chacun d'eux dépend du choix de représentation du graphe et de la structure même du graphe.
| ALGORITHME DE KRUSKAL |
Le principe de l'algorithme de Kruskal pour trouver un arbre de poids minimum dans un graphe G est tout d'abord de trier les arcs par ordre croissant de leur poids. Ensuite, dans cet ordre, les arcs sont ajoutés un par un dans un graphe G' pour construire progressivement l'arbre. Un arc est ajouté seulement si son ajout dans G' n'introduit pas de cycle, autrement dit, si G' reste un arbre. Sinon, on passe à l'arc suivant dans l'ordre du tri.
| Algorithme |
Titre: Kruskal
Entrées: G = (X;U) un graphe.
Sortie: U' un ensemble d'arcs.
Variables intermédiaires: i un entier.
Début
trier les arcs de G dans l'ordre croissant des poids;
[On les notera u1, u2, ... , um.]
U' ![]()
![]() ;
;
pour i ![]() 1 à m faire
1 à m faire
si le graphe (X;U' ![]() {ui}) ne contient pas de cycle alors
{ui}) ne contient pas de cycle alors
U' ![]() U'
U' ![]() {ui};
{ui};
fin si;
fin tant que;
Fin
| Justification |
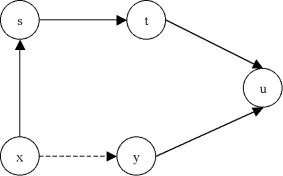
Supposons que l'algorithme est effectué quelques itérations. Considérons maintenant l'ajout de l'arc u = (x;y) dans l'arbre. On suppose que cet ajout n'introduit pas de cycle dans G'. Est-on certain que u permet la construction de l'arbre de coût minimum ? En fait, x et y doivent être connectés d'une manière ou d'une autre. Donc si ce n'est pas u qui les relie, ce sera une autre chaîne C = (x,s,t,u,y) de x à y comme le montre la figure ci-dessous. Comme u n'introduit pas de cycle, cette autre chaîne n'est pas encore construite, elle le sera plus tard. Cela signifie que tous les arcs de cette chaîne ont un coût supérieur ou égal à celui de u. Donc, le fait de choisir la chaîne C pour connecter x à y est plus onéreuse que de connecter x à y par u. En effet, supprimons n'importe quel arc de la chaîne C et remplaçons le par u. On obtiendra toujours un arbre mais de coût plus faible. Cela justifie le choix de u et donc la démarche globale de l'algorithme de Kruskal.
| ALGORITHME DE PRIM |
Le principe de l'algorithme de Prim pour trouver un arbre de poids minimum dans un graphe G est de fusionner, deux par deux les noeuds de G pour obtenir finalement un arbre. Par fusionner, on entend remplacer deux noeuds par un seul. Tous les arcs adjacents à l'un ou l'autre des anciens noeuds deviennent adjacents au nouveau noeud. Le choix des noeuds que l'on fusionne est fait en choisissant au hasard un noeud et en cherchant un arc adjacent (autre qu'une boucle) qui a le coût le plus faible. Ce qui fournit le deuxième noeud de la fusion.
| Algorithme |
Titre: Prim
Entrées: G = (X;U) un graphe.
Sortie: U' un ensemble d'arcs.
Variables intermédiaires: x un noeud, u un arc.
Début
U' ![]()
![]() ;
;
tant que |U'| < n - 1 faire
choisir x ![]() X;
X;
choisir u ![]() U | u = (x;y) ou u = (y;x) avec y
U | u = (x;y) ou u = (y;x) avec y ![]() x
x
et coût(u) = min{coût(v) | v ![]() U avec
v = (x;y) ou v = (y;x), x
U avec
v = (x;y) ou v = (y;x), x ![]() y};
y};
U' ![]() U'
U' ![]() {u};
{u};
fusionner x et y; [x et y deviennent un seul noeud.]
fin tant que;
Fin
| Justification |
Tout d'abord, si on choisit un arc u = (x;y) où x et y sont des noeuds qui ne sont pas le résultat d'une fusion, on peut dire que le graphe résultant ({x,y};{u}) est un arbre de poids minimum.
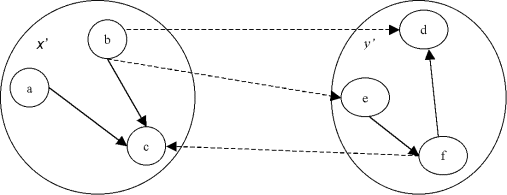
Maintenant, si on choisit un arc u = (x';y') où x' et y' sont des noeuds qui sont le résultat de fusions, la figure ci-dessous peut représenter la situation. En fait, x' et y' représentent des arbres de poids minimum (hypothèse de récurrence). Si u' est l'arc entre x' et y' de poids minimum, le graphe ({a,b,c,d,e,f};{(a;c),(b;c),(d;f),(e;f),u}) sera un arbre de poids minimum. Donc à la dernière étape de l'algorithme, on obtiendra bien un arbre de poids minimum qui est un graphe partiel de G.
|