|
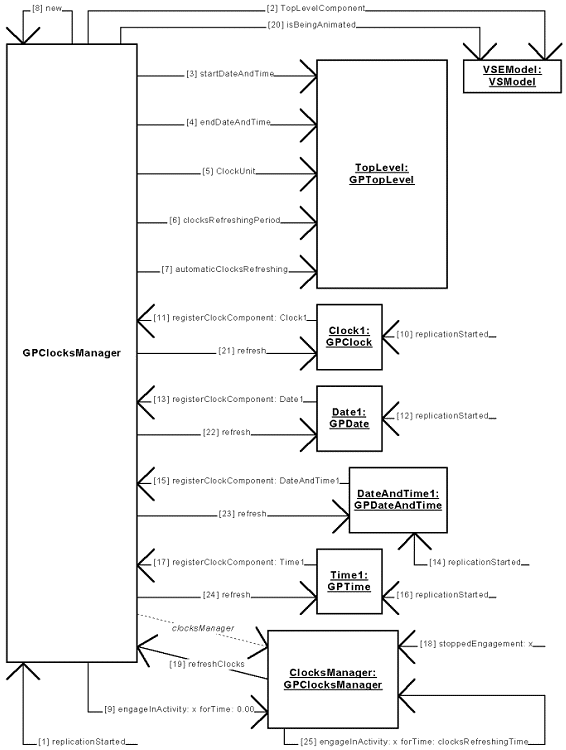
6. DESIGN OF LIBRARIES OF REUSABLE COMPONENTS |
| INTRODUCTION |
In this chapter, we present the libraries developed during the internship. For each one, we introduce the palette of available components, the class hierarchy of the library and some collaboration diagrams that explain, based on examples, how the library works. Some algorithms are also briefly explained. Finally, we present examples of reuse of these libraries. But before this presentation, a short description of the formalism used is introduced.
Two annexes are also available in direct relation with the study. Annex A contains the source code of some methods written with the VSE language, which presents algorithms of general purpose that can easily be reused and adapted to another language. Annex B contains the dictionary of the libraries. There is an exhaustive list of all the methods and attributes of each class created in the libraries and for each one a brief description. The aim of this annex is to give complementary details to the presentation of this chapter.
| FORMALISM |
The formalism used here is inspired from the Unified Modeling Language (UML) (see [OMG Web]). Some adaptations have been made according to the specificity of VSE. Hence, we present here the three different kinds of diagram we will use to explain a model or a library. There are the class hierarchy, the component hierarchy and the collaboration diagrams.
| Class Hierarchy Diagram |
This diagram introduces the graph of inheritance of the classes. The inheritance relationship is symbolized as shown by Figure 33. The arrow represented the inheritance shows the superclass with its end extremity and the subclass with its start extremity. Finally, the boxes represent the classes. In the class hierarchy diagram, the attributes and the methods of each class are also represented (see Figure 34). Words in italic font are attribute descriptions, whereas the words in normal font are method descriptions. Our formalism describes an attribute by giving its name then its type, both separated by a colon. For readability reasons, only the name of the methods is given, with the same syntax as in the VSE language. A colon in the name of a method indicates that it needs an argument. However, to know the type of an argument, the reader must consult the dictionary of the libraries in annex B.
Figure 33: Formalism of the Inheritance Relationship.
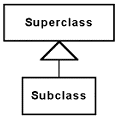 |
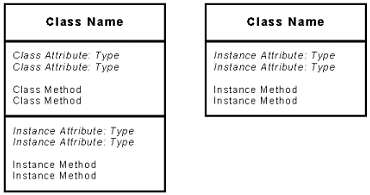
Figure 34 presents two ways to describe a class. The first, on the left, represents a class having both class and instance characteristics, whereas the other one represents a class with only instance characteristics. In the first case, the upper box is for the class methods and attributes and the lower one for the instance characteristics. In the second case, there is only one box for the instance attributes and methods.
Figure 34: Formalism of a Class.
 |
In VSE, an attribute or an argument of a method can have a standard type, like integer or real, or can be a reference to an object of a given class. For instance, an attribute referencing a shape will have the type VSShape reference. In our presentation, we will never specify the term reference. It will be implicit that attributes and arguments representing objects are in fact object references, and not the objects themselves.
Figure 35 presents how our formalism represents some particular cases. The first is the notation for the overridden methods. We saw earlier that it is possible to modify or replace a method inherited from a superclass. In our formalism, when an asterisk is put after the name of a method in the class hierarchy diagram, that means the method has been overridden. The subclass brings new features, a new behavior for this method. However it does not specify if the method is totally replaced or just completed.
Another particular formalism is the representation of a collection of objects. During the presentation of VSE, we saw that the standard library provides classes to represent a collection of objects. The metaclass for that is VSContainer and two subclasses allow the instantiation of two kinds of object: a list (VSList) or a dictionary (VSDictionary). The access to the objects can be performed sequentially or directly by giving the position of the object in the list, or its key if it is in a dictionary. To represent a collection of objects, we choose the formalism presented by Figure 35. The attributes in this example represent respectively a list of integers and a dictionary of shapes. First the type of the container is indicated, and then, between brackets, the type of the collected objects is defined.
Figure 35: Formalism of Some Specific Attributes and Methods.
 |
| Component Hierarchy Diagram |
We have seen that a model has a hierarchy of components due to the fact that a component can be decomposed. Figure 37 shows the formalism chosen to represent this kind of decomposition. A component hierarchy deals with objects whereas the class hierarchy deals with classes. Then, we will see that a collaboration diagram can deal with both the classes and the objects. Hence, a different notation is used to represent a class or an object. Classes and objects are represented by a box, but the name of the objects is underlined. Figure 36 represents an object with the left box and a class with the other one. Moreover, to describe an object, both its name and its class are specified. First the name is written and then, separated by a colon, the name of the class is indicated.
Figure 36: Formalism of an Object.
Figure 37 presents an example of decomposition of components, representing a component hierarchy. An arrow formalizes the relationship of decomposition. The start extremity of the arrow points the object that is decomposed and the end extremity of the arrow points the object belonging to this decomposition.
Figure 37: Formalism of a Component Hierarchy Diagram.
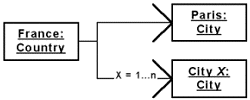 |
A component can possess several times the same kind of object. For this reason, if is possible to indicate how many times the relationship exists. In our example, we see that the component France of the class Country has a capital and several other cities, all of the class City.
| Collaboration Diagram |
Collaboration diagrams present examples of the behavior of a part of a model. Usually it deals with instances, but sometimes classes are directly implied. A collaboration diagram shows the sequence of messages exchanged between objects and classes, considering a particular case. Hence, through several examples explained by collaboration diagrams, it is possible to present in details the behavior of a model or a library of components.
Figure 38: Formalism of a Collaboration Diagram.
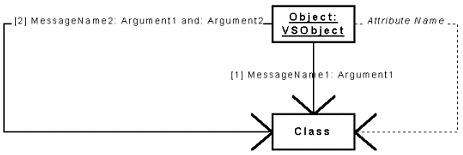 |
Figure 38 presents the formalism of a collaboration diagram. As the class hierarchy and component hierarchy diagrams, a box represents either an object or a class. Then, a sequence of message exchanges is represented. An arrow specifies a message passing. Its start extremity points the object or the class sending the message, and its end extremity points the entity receiving the message. Messages are numbered to indicate the chronology of the message exchanges. The name of the message is written near the arrow and the arguments are also showed using the formalism of the VSE language. Arrows with a discontinuous line represents a reference to an object. That means the object or class the arrow starts from references the other object, i.e. an attribute of the first object references the other one.
| THE SPOT LIBRARY |
| Introduction |
For the purpose of animation or not, the movement of dynamic objects in a layout can be complex to manage. In fact, there can be a lot of interactions between the dynamic objects. That means the designer will spend a long time to find a way to model the movement and validate it. The aim of this library is to provide a generic solution for the movement of dynamic objects in a layout, with as less programming as possible during the reuse step. This library can be used both for the purpose of animation and for a real need in the modeling.
To present this library, we first introduce briefly each template provided in the palette of the library. The templates allow the building of a graph, a network of spots, to describe the movement of dynamic objects in the layout of a component, and the control of these movements with as less programming as possible. Then, we will present some collaboration diagrams to explain more precisely the internal behavior of the library. Finally, we will discuss briefly about the algorithm used to allow a dynamic object to move by itself to its next destination.
This library appears to be time consuming, so the aim of such a detailed presentation of the internal behavior of the library is to bring information to show what has been done and what can be done to ameliorate, optimize the library. We will see that we have chosen here the assurance of no blocking of the dynamic objects opposed to fast algorithms. The names of the classes and types defined in this library begin with the letters SP.
| Palette |
Figure 39: Palette of the Spot Library.
 |
| The SPDynamicObject Component |
The purpose of this library is the movement of dynamic objects in a layout. To use correctly the library, a dynamic object must belong to the SPDynamicObject class or one of its subclasses. It is a specialization of the standard VSDynamicObject class. The aim of this library is to provide a way to let dynamic objects moving autonomously. By autonomous we mean, giving the object a destination spot and a reference moving time, corresponding to its moving speed, the object is able to reach its target as soon as possible, following a given set of rules.
To control movements, a dynamic object has many attributes we describe here. First, it has a priority level that offers an object to have the priority upon another one to move. Then, a dynamic object belongs to a group identified by a number. It is a way to distinguish objects and apply different rules upon them. Another attribute a dynamic object possesses is a moving direction. It comes from the example of the airplane. The same way is used by the passengers to go to their seat during the boarding and to leave them during the landing. So, we will speak of normal direction and inverse direction. We will describe this notion later when explaining the SPLink component.
| Graph of Spots |
To define the rules of moving, the user must first build a graph, a network of spots. A spot represents a point where a dynamic object can move. To move from a spot to another, spots are linked. Two spots are linked means that there is a way for a dynamic object to move directly from one spot to another.
| The SPSpot Component |
A spot is more precisely a point where a dynamic object can come. After its arrival, a dynamic object can undergo any kind of operation. The library provides different types of spot: SPMoveSpot, SPChangePrioritySpot, SPEntranceSpot, SPExitSpot and SPComponent. We describe them now.
| The SPMoveSpot Component |
It is a spot where arriving dynamic objects are automatically, and as soon as possible, moved to their next destination. There are three kinds of move spot provided by the library.
SPChangePrioritySpot, that is a move spot where the priority level of a dynamic object is changed to a another one. The aim of this component comes from the road intersection problem with the case of a stop. Placed at the right places, spots of this kind will increase the priority of the vehicles arriving from the road with priority.
SPEntranceSpot, that is a move spot through which a dynamic object enters into a graph of spots.
SPExitSpot, that is a move spot through which a dynamic object leaves a graph of spots. It is associated with a shape. A dynamic object arriving at an exit spot moves automatically to the associated shape outside the graph.
| The SPComponent Component |
This component is a spot. When a dynamic object arrives on it, it is placed in a list of waiting objects to be served. These objects wait for undergoing an operation. That means the user of the library will have to define the operation to perform and when a dynamic object becomes available to move to another component.
| The SPLink Component |
A link associates two spots. It indicates that a dynamic object can move between them. However, two spots A and B are linked does not mean that a dynamic object can move both from A to B and from B to A. In fact, a link can be unidirectional or bidirectional. Figure 40 presents the two kinds of link represented by a line for the bidirectional link and an arrow for the unidirectional link. Let us explain now the notion of normal or inverse direction of a dynamic object. If we consider the unidirectional link, a dynamic object with a normal direction is allowed to move from A to B, but not from B to A. If the dynamic object has an inverse direction, it is allowed to move from B to A, but not from A to B. The example of the airplane is presented further and illustrates this possibility.
Figure 40: Unidirectional and Bidirectional Links.
 |
The notion of distance is introduced between two spots. For that, each link has a moving coefficient. An object using a link will move using a time corresponding to its reference moving time multiplied by the moving coefficient of the link. Usually, the reference moving time of a dynamic object represents the time to move along a unit of distance, i.e. its speed, and the moving coefficient of the link represents the distance between two spots. The moving time of a dynamic object is a random variable, whereas the moving coefficient of a link is a real number. Finally, a link belongs to a group. For that, it has an attribute, as the dynamic objects, that is a number and represents a group. The rule associated is that a dynamic object can only use the links belonging to its group. That allows moving different kinds of object through the same spots but using different ways.
| The SPAuthorization Component |
A link can be associated with one or more SPAuthorization components. Such components have two statuses: "accepted" or "refused". A link can be used by a component only if all the authorizations associated with it are accepted. This comes from the lights at a road intersection. Vehicles stop when the light is red, i.e. the authorization is refused, and move when the light is green, i.e. the authorization is accepted. The user of the library will have to define the rules of acceptation and refusal of an authorization.
| The SPInterference Component |
A link represents physically or logically a way between two spots. But it can appear that two links intersect as shown by Figure 41. In this case, the notion of interference is introduced. An interference regroups the links that can not be used at the same time. In our example, when a dynamic object uses the link 1, the link 2 is unusable, so an interference object will be created to associate these two links and forbid their mutual use. The priority of the dynamic objects is also considered with the interference. In our example, if we imagine a dynamic object in the source spot of the link 1 and another one in the source spot of the link 2. The object that will move is the one that has the highest priority.
Figure 41: Intersection of Links.
 |
| The SPSupervisor Component |
The supervisor component is used to supervise the movement of dynamic objects in a graph. In fact, spots can be ordered to indicate to a supervisor about the objects arriving in it or leaving it. By this way, it is possible to collect data for further analysis, or simply detect a particular event. For instance, the user might want to stop the simulation after the arrival of a given number of dynamic objects in a particular component. Another example is the case of the airplane. It seems interesting to detect when all the passengers are seated. So, all the seats are ordered to inform a common supervisor when a passenger arrives to its seat.
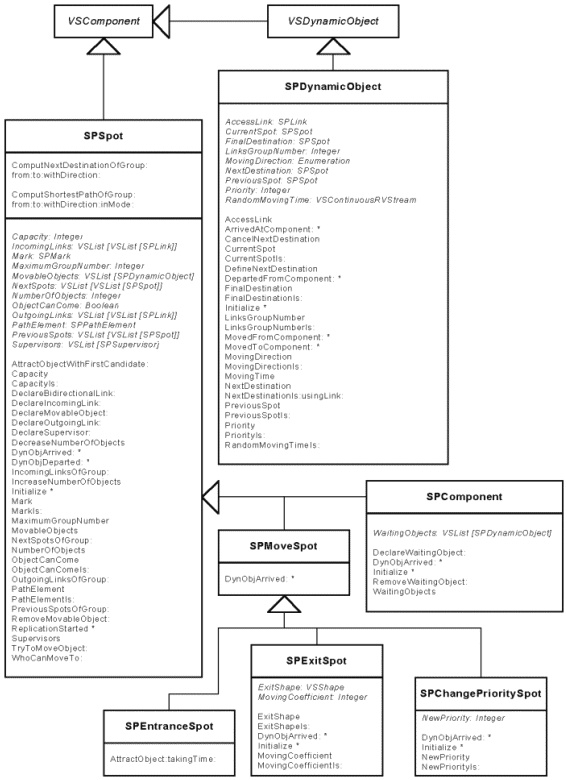
| Class Hierarchy |
Figure 42: Class Hierarchy of the Spot Library - Part I.
 |
Figure 43: Class Hierarchy of the Spot Library - Part II.
 |
| Collaboration Diagrams |
| Arrival of a SPDynamicObject at a SPMoveSpot |
Figure 44: Spot Library - Collaboration Diagram 1.
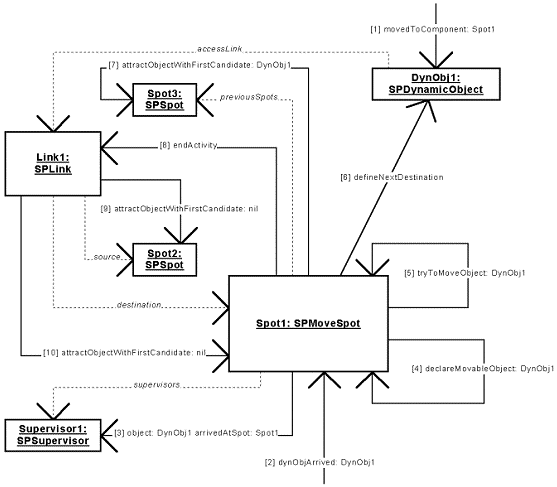 |
Figure 44 presents the collaboration diagram in the case of a dynamic object DynObj1 arriving to a move spot Spot1. We suppose the spot is shallow. The case of a deep spot is not presented here. The messages exchanged are a bit different but the logic stills the same. The following messages are exchanged between the components. First the simulator informs the move spot and the dynamic object of the arrival.
1.
Simulator [DynObj1 movedToComponent: Spot1]
[DynObj1 movedToComponent: Spot1]
The simulator automatically sends this message to the dynamic object when it arrives at the move spot. The dynamic object just updates its attributes.2.
Simulator [Spot1 dynObjArrived: DynObj1]
[Spot1 dynObjArrived: DynObj1]
The simulator automatically sends this message when a dynamic object arrives at the move spot. The spot informs its supervisors that a dynamic object has arrived (message 3), adds the dynamic object to the list of the objects allowed to move to their next destination (message 4) and tells the link that its activity is ended (message 8).3.
Spot1 [Supervisor1 object: DynObj1 arrivedAtSpot: Spot1]
[Supervisor1 object: DynObj1 arrivedAtSpot: Spot1]
The spot informs all its supervisors of the arrival of the dynamic object. In this example, there is only one supervisor.4.
Spot1 [Spot1 declareMovableObject: DynObj1]
[Spot1 declareMovableObject: DynObj1]
The dynamic object is added to the list of the objects allowed to move to their next destination. Immediately, the spot tries to move the object to its next destination (message 5), because a move spot is just a point the dynamic objects passes through. The less time they stay in a move spot, the better.5.
Spot1 [Spot1 tryToMoveObject: DynObj1]
[Spot1 tryToMoveObject: DynObj1]
The spot tries to move the object to its next destination. For that, the dynamic object must first of all determine its next destination (message 6). Then, the destination spot defined is ordered to attract an object with the privileged candidate DynObj1 (message 7). If no dynamic object with a higher priority wants to move to the same spot, DynObj1 will move to the spot, else the logic of the tryToMoveObject: method is reiterated, i.e. the dynamic object chooses again its next destination and so on.6.
Spot1 [DynObj1 defineNextDestination]
[DynObj1 defineNextDestination]
The dynamic object finds its best next destination. For that, the shortest path between the dynamic object and its final destination is found. If the next spot in this path is available, the dynamic object chooses this spot as next destination. Else, if it is not available, the dynamic object looks at each next spot it can reach. If one of the next spots is its final destination, it waits for the destination to be available, else it selects the available spot that is the nearest to the final destination, but avoids the ones that have the current spot in their shortest path to the final destination. That avoids a dynamic object to move cyclically between two spots.7.
Spot1 [Spot3 attractObjectWithFirstCandidate: DynObj1]
[Spot3 attractObjectWithFirstCandidate: DynObj1]
The spot tries to attract an object. For that, it chooses a dynamic object with the highest priority that can come from the adjacent spots. This method is detailed further in another collaboration diagram about the attraction of an object, because it induces a lot of messages to the neighbor spots.8.
Spot1 [Link1 endActivity]
[Link1 endActivity]
When the dynamic object arrives at the spot, the link it has used must be freed. For that, the message endActivity is sent to the used link. The link becomes available and it orders its source and destination spots to attract an object, because the fact the link was used may has blocked a dynamic object in one of these spots. In the same way, the spots of the links implied in an interference with this link are asked to attract also an object, because an object can still be blocked.9.
Link1 [Spot2 attractObjectWithFirstCandidate: nil]
[Spot2 attractObjectWithFirstCandidate: nil]
Spot2 is ordered to attract an object without any privileged candidate.10.
Link1 [Spot1 attractObjectWithFirstCandidate: nil]
[Spot1 attractObjectWithFirstCandidate: nil]
| Arrival of a SPDynamicObject at a SPComponent |
Figure 45: Spot Library - Collaboration Diagram 2.
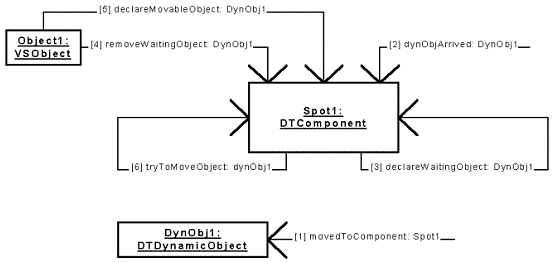 |
When a dynamic object arrives at a SPComponent spot, the object is not placed directly in the list of the objects allowed to move to their next destination. They are placed in a list of waiting objects. Then, they undergo an operation, and after that, they are allowed to move to their next destination. Of course, this behavior must be completely defined by the user. Let us see what happens when a dynamic object arrives (see Figure 45). First the simulator informs the dynamic object and the spot of the arrival.
1.
Simulator [DynObj1 movedToComponent: Spot1]
[DynObj1 movedToComponent: Spot1]
Exactly the same things happen as for the move spot. The simulator automatically sends this message to the dynamic object when it arrives at the move spot.2.
Simulator [Spot1 dynObjArrived: DynObj1]
[Spot1 dynObjArrived: DynObj1]
It is similar to the case of the move spot. The simulator automatically sends this message when a dynamic object arrives at the move spot. The spot informs its supervisors that a dynamic object has arrived. But in this case there is no supervisor. Then, it adds the dynamic object to the list of the objects waiting for undergoing an operation (message 3), which is the difference with a move spot. Finally, it tells the used link that its activity is ended (it is not represented here because it is exactly the same as the case of the move spot).3.
Spot1 [Spot1 declareWaitingObject: DynObj1]
[Spot1 declareWaitingObject: DynObj1]
The dynamic object is added to the list of the waiting objects for undergoing an operation.4.
Object1 [Spot1 removeWaitingObject: DynObj1]
[Spot1 removeWaitingObject: DynObj1]
The dynamic object DynObj1 will undergo an operation, expressed somewhere in the model. After the operation, the Spot1 receives the order of remove the object DynObj1 from the list of the waiting objects.5.
Object1 [Spot1 declareWaitingObject: DynObj1]
[Spot1 declareWaitingObject: DynObj1]
The dynamic object is now placed in the list of the objects allowed to move to their next destination. Exactly the same process as for the move spot is performed, i.e. the Spot1 is ordered to try to move the object (message 6).6.
Spot1 [Spot1 tryToMoveObject: DynObj1]
[Spot1 tryToMoveObject: DynObj1]
This method is not detailed and corresponds exactly to the previous case of the move spot.
| Departure of a SPDynamicObject From a SPSpot |
Figure 46: Spot Library - Collaboration Diagram 3.
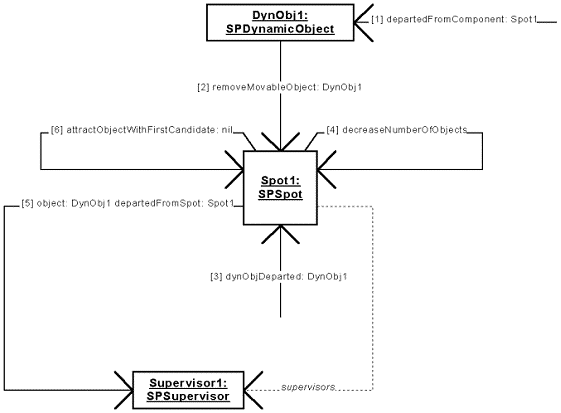 |
Figure 46 represents what happens when a dynamic object leaves a spot. First, the simulator informs the dynamic object and the spot of the departure.
1.
Simulator [DynObj1 departedFromComponent: Spot1]
[DynObj1 departedFromComponent: Spot1]
This method is called when the dynamic object has left the spot. It updates the attributes of the dynamic object, and tells the left spot to remove the object from the list of the objects allowed to move to their next destination (message 2).2.
DynObj1 [Spot1 removeMovableObject: DynObj1]
[Spot1 removeMovableObject: DynObj1]3.
Simulator [Spot1 dynObjDeparted: DynObj1]
[Spot1 dynObjDeparted: DynObj1]
The simulator automatically calls this method when a dynamic object has left the spot. The spot decreases the number of dynamic objects in it (message 4), informs its supervisors of the departure (message 5), and then tries to attract another object (message 6).4.
Spot1 [Spot1 decreaseNumberOfObjects]
[Spot1 decreaseNumberOfObjects]
An object has left the spot, so the number of objects must be decreased.5.
Spot1 [Supervisor1 object: DynObj1 departedFromSpot: Spot1]
[Supervisor1 object: DynObj1 departedFromSpot: Spot1]
The supervisor is informed of the departure of the dynamic object from the spot.6.
Spot1 [Spot1 attractObjectWithFirstCandidate: nil]
[Spot1 attractObjectWithFirstCandidate: nil]
Spot1 is ordered to attract an object without any privileged candidate.
| Attraction of a SPDynamicObject |
Figure 47: Spot Library - Collaboration Diagram 4.
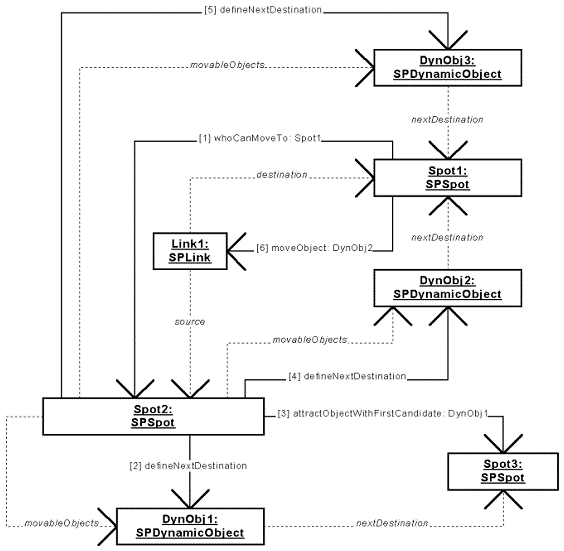 |
When a spot is ordered to attract an object, it has to choose the dynamic object with the highest priority that wants to move to it. The method called to attract an object is attractObjectWithFirstCandidate:. The calling object can specify a privileged candidate to attract, i.e. if no dynamic object with a higher priority is found, it is this one that will move. When receiving the message, the attracting spot exchanges the following messages to each spot susceptible of having an object that wants to move to the considered attracting spot.
1.
Spot1 [Spot2 whoCanMoveTo: Spot1]
[Spot2 whoCanMoveTo: Spot1]
For each adjacent spot, the attracting spot asks which dynamic object in the adjacent spot has the highest priority and wants to move to the attracting spot. So, the adjacent spot looks each dynamic object it possesses and asks the dynamic object its next destination (message 2) and its priority. If the next destination of the object is not Spot1, the spot destination of the object is ordered to attract an object (message 3) with the dynamic object as privileged candidate.2.
Spot2 [DynObj1 defineNextDestination]
[DynObj1 defineNextDestination]
The dynamic object DynObj1 selects its next destination. See the previous collaboration diagrams for more explanations.3.
Spot2 [Spot3 attractObjectWithFirstCandidate: DynObj1]
[Spot3 attractObjectWithFirstCandidate: DynObj1]
The next destination of the dynamic object DynObj1 is not the attracting spot, so the next destination spot is asked to attract a dynamic object, because the dynamic object considered can have been blocked by the attracting spot, and now it wants to move to another spot.4.
Spot2 [DynObj2 defineNextDestination]
[DynObj2 defineNextDestination]
The next destination of DynObj2 is the attracting spot, so this object can be a candidate.5.
Spot2 [DynObj3 defineNextDestination]
[DynObj3 defineNextDestination]
The next destination of DynObj3 is the attracting spot, but DynObj2 has a higher priority so the best candidate is DynObj2.
This previous sequence of messages is performed for each spot that can have an interesting dynamic object. Finally, the attracting spot will have the choice between dynamic objects of several spots with the same priority. Randomly, but uniformly, a dynamic object is chosen among them. Then, this dynamic object is moved (message 6).
6.
Spot1 [Link1 moveObject: DynObj2]
[Link1 moveObject: DynObj2]
When a dynamic object defines its next destination by the defineNextDestination method, it also defines which link it must use. Hence, when a spot chooses a dynamic object to move, it knows which link to use to move the object. This is detailed in the next collaboration diagram.
| Movement of a SPDynamicObject Through a SPLink |
Figure 48: Spot Library - Collaboration Diagram 5.
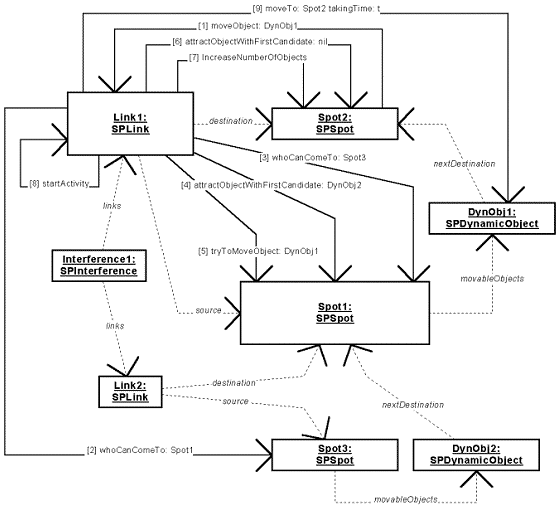 |
Figure 48 presents the case when a link is ordered to move an object through the method moveObject:. But the problem is that some links can interfere, which means some dynamic objects in other spots can have a better priority than the dynamic object chosen to move. Before moving the object, the link must be sure that no dynamic object in the spots associated with some interfering link has a higher priority. Starting from the message moveObject:, the following messages are exchanged.
1.
Spot2 [Link1 moveObject: DynObj1]
[Link1 moveObject: DynObj1]
For each couple of spots associated with an interfering link, the message whoCanComeTo: (messages 2 and 3) is sent. As explained previously, this message can induce an attraction by another spot and makes a lot of changes in the graph. So when the messages 2 or 3 return their answer, Link1 must verify that DynObj1 did not move, that its destination stills available and that itself, the link, stills usable.
In the case of a positive verification, the messages 2 and 3 can return a better candidate DynObj2 than DynObj1. In this case, the destination of this new candidate, Spot1 for instance, is asked to attract an object with the privileged candidate DynObj2 (message 4). Lots of changes can occur then as explained in the previous collaboration diagrams. So after this message 4, the same verifications as after the messages 2 and 3 must be performed.
In the case of a failure of the verification, a message will be sent to the spot where DynObj1 is located, in order to try to move the object (message 5). The destination of DynObj1 is also ordered to attract another object because maybe another object can come to it instead of DynObj1 (message 6).
If, after all the candidates tested and moved, DynObj1 stills in Spot1, if Spot2 and Link1 stills available, Link1 will reserve a place in the destination spot (message 7), reserve the link (message 8) and move DynObj1 (message 9).2.
Link1 [Spot3 whoCanMoveTo: Spot1]
[Spot3 whoCanMoveTo: Spot1]3.
Link1 [Spot1 whoCanMoveTo: Spot3]
[Spot1 whoCanMoveTo: Spot3]4.
Link1 [Spot1 attractObjectWithFirstCandidate: DynObj2]
[Spot1 attractObjectWithFirstCandidate: DynObj2]5.
Link1 [Spot1 tryToMoveObject: DynObj1]
[Spot1 tryToMoveObject: DynObj1]6.
Link1 [Spot2 attractObjectWithFirstCandidate: nil]
[Spot2 attractObjectWithFirstCandidate: nil]7.
Link1 [Spot2 increaseNumberOfObjects]
[Spot2 increaseNumberOfObjects]
This method increases the number of objects in the spot. When this number reaches the capacity of the spot, the boolean number objectCanCome is set to false, meaning that no other object can come to the spot.8.
Link1 [Link1 startActivity]
[Link1 startActivity]
The link is reserved. No other dynamic object can use it. By the same way, the interfering links can not be used, because before using them, it will be tested if one of the interfering links, especially Link1, is used.9.
Link1 [DynObj1 moveTo: Spot2 takingTime: t]
[DynObj1 moveTo: Spot2 takingTime: t]
The dynamic object is finally moved to its next destination. The time needed to move is determined as following. The attribute movingTime is a random variable and represents the reference moving time (the speed) of the dynamic object. So a realization of it is taken and multiplied by the moving coefficient (the length) of the link.
| Search of a Shortest Path in a Graph of Spots |
We present briefly the algorithm used to determine the shortest path a dynamic object can use to move from a spot to another. In fact, the library uses often this algorithm, so it needs to be as fast as possible. In fact, every time the method defineNextDestination of a dynamic object is called, this algorithm is run at least one time.
A classical algorithm has been adapted. First of all, the graph of spots used is constructed at the beginning of the simulation and never changes. During a search, spots are marked, but at each new search the spots need to be unmarked. That supposes a process to unmark each spot of the graph. That can take some time. The first adaptation is to add an attribute to each spot, a mark. It is a reference to an object of the class SPMark. This class has no particularity. The aim is to mark the spot with a new object at each new search. At the beginning of the search, a new object is created and its reference is used to mark the spots. In other word, if a spot has a mark reference different from the current mark, the spot is not marked.
Moreover, with VSE, the memory used by the objects is freed by a garbage collector, meaning that an object stills in the memory until nobody references it. So, the mark of a previous search stills in the memory until no spot references it. That means a same mark will be reused only if no spot uses the mark at the beginning of a search. Hence, there will be no conflict and the mark we have defined is surely unique.
Then, to avoid the use of lists, that are extremely time consuming with VSE, another attribute is added to each spot. It is an object of the class SPPathElement. This object contains the following information.
The shortest distance found so far to the start spot.
The path element of the spot used to access the current spot by the shortest path found so far.
The link used to access the current spot by the shortest path found so far.
During the search, this information is updated. Hence, only one list is managed, a list of unexplored spots, but it is used as a queue, which is not very time consuming. At the end of the search, we just need to consider the destination spot and follow the path in the inverse direction through the path elements.
The principle of the algorithm is that knowing, for a given spot, its distance to the start point, it is possible to determine the distance to the start of each spot adjacent, supposing an arrival from the current spot considered. If this distance is better than the best distance known so far for the adjacent spot, the path element of the adjacent spot is updated. If the adjacent spot is unmarked, it is also put in a list of unexplored spots. The algorithm loops until this list is empty. At each iteration, a spot is removed from this list, marked and the process explained previously is performed. The first spot considered is the start spot given for the search.
Algorithm A.1 of annex A presents the method with the VSE language. The parameters the user must give are the start spot, the destination spot, and the group number of the dynamic object that will use the path, and also its moving direction. Finally, it is possible to find a path considering the current state of the graph, meaning considering that some spots or links are unusable.
| Airplane Model |
This model represents the inside of an airplane as shown by Figure 49 and Figure 50. The purpose of this model is to simulate the movement of passengers in an airplane during the boarding, when the passengers enter the airplane and move to their seat, and during the landing, when the passengers leave their seat to go to the exit of the airplane. The spot library has been used to build the model and we will see now what has been added to the library to obtain the model.
Figure 49: Inside of an Airplane.
 |
When looking at the class hierarchy diagram (see Figure 51), we note that there is only four new classes. The purpose of three of them is obvious: Airplane, Passenger and Seat. They are induced by the nature of the system to model. But the class AirplaneSupervisor is not a natural approach and is due to the nature of the spot library.
Figure 50: Component Hierarchy of the Airplane Model.
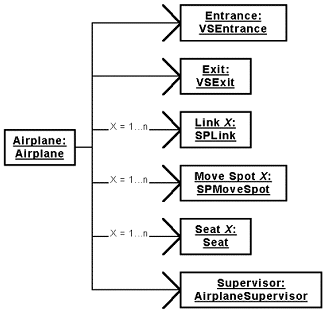 |
The dynamic objects moving in the airplane are the passengers, so they must inherit from SPDynamicObject, but no particular behavior or attribute is added. This class is defined only for the clarity of the model. The seats are the destinations of the passengers, so they need to belong to the class SPSpot, and more precisely, they belong to the class SPComponent, because passengers need to wait when they arrive at their seat.
Figure 51: Class Hierarchy of the Airplane Model.
 |
Then, the class Airplane is defined to represent the top-level component of the model and generate the passengers that will enter into the airplane. Finally, the model will simulate cyclically a boarding then a landing, so the detection of the following events must be done.
All the passengers are seated.
All the passengers have left the airplane.
For this detection, a SPSupervisor object is needed. To use it, there is no choice but specializes it, because no behavior is defined when the supervisor receives messages from the spots. The supervisor will receive messages from the seats and from the exit spot of the airplane. Respectively, the passengers arriving to their seat and the passengers leaving the airplane are counted. When the number reaches the total number of passengers, respectively a landing or a boarding is ordered.
To start a boarding, 36 passengers are created and each one is assigned randomly to a seat, i.e. its FinalDestination attribute is set to this seat. The moving direction of the passengers is the normal direction. Then, each one of them is entered in the graph through the entrance spot. As expected, each passenger moves automatically to its seat. To start a landing, the moving direction of each passenger is set to the inverse direction. Then, the exit spot of the airplane is assigned as the final destination of each passenger. Finally, the move spots near the seats are ordered to attract an object. As expected, the passengers left their seat in a random order and use the links of the graph in their inverse direction until the exit spot of the airplane.
| Road Traffic Model |
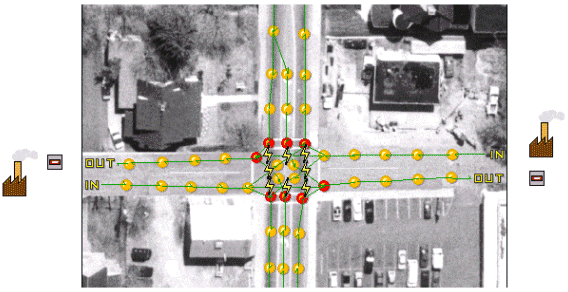
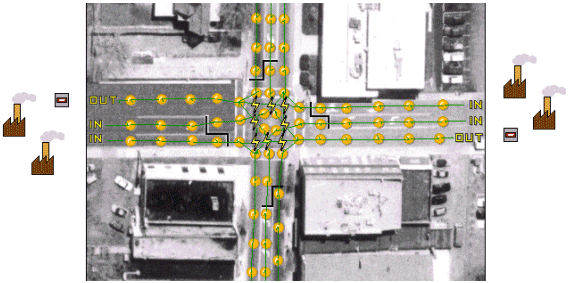
The purpose of this model is to simulate the movement of vehicles in the town of Blacksburg. Figure 52 and Figure 53 show two intersections. The first shows an intersection with stops and the other one shows an intersection with lights. The objects symbolized by a manufacture will generate vehicles that will move in the street, respecting priorities and lights. This model uses the spot library. Only few classes have been added.
 |
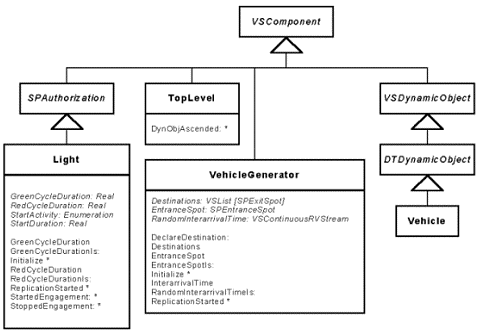
As the airplane model, only four classes have been created (see Figure 54). Two of them seem completely natural: Light and Vehicle. The Light class inherits from the SPAuthorization class. In fact, a light is naturally an authorization or a refusal. In this model, the light is an object that just changes its status cyclically, from "accepted" to "refused", corresponding respectively to a green or red light. A Vehicle class has been created, only for the clarity of the model. It inherits from the SPDynamicObject class to be able to use the spot library.
Figure 53: Light Intersection.
 |
Then, two classes less obvious have been developed. One to represent the top-level component of the model, i.e. the town of Blacksburg, and the other one to simulate the arrival of vehicles in the model. The VehicleGenerator class represents objects that will create continuously vehicles using a random variable for the inter-arrival time.
Figure 54: Class Hierarchy of the Road Traffic Model.
 |
As shown by Figure 55, SPInterference objects are used to represent the intersection of several ways. SPChangePriority objects are also used for the stop intersection. A vehicle has a final destination, but the way it will use to move to this destination is not always known. A priori, we do not know which vehicle will have the priority upon another one. Hence, the idea with the SPChangePrioritySpot components is to put some spots of this kind on the road having the highest priority, just before the intersection and just after. The first ones will increase the priority of the vehicles passing on them and the other ones will surrender their normal priority to the vehicles. By this way, the vehicles having the lower priority will let the other vehicles pass. In our model, SPChangePriority objects are also put in the way of the lower priority vehicles to decrease their priority. It is not necessary, but it avoids controlling the default priority level at the vehicle generators. In Figure 52, the SPChangePrioritySpot objects are the darker move spots.
Figure 55: Component Hierarchy of the Road Traffic Model.
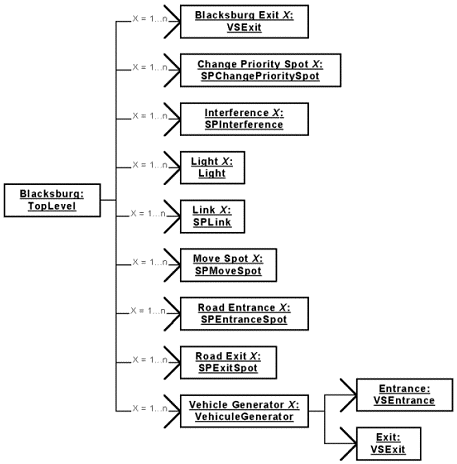 |
During the simulation, vehicles are regularly created and assigned randomly to a final destination, an exit spot representing the end of a street. Then, the vehicles enter the graph of spots. As expected, vehicles move to their final destination, respecting the lights and the spots. Finally, we can see that there is no visual collision of the vehicles.
| Conclusion |
This library provides a full set of components and classes that allows expressing a lot of various rules for the movement of dynamic objects in a layout. The user does not need a lot of time to model the movement of dynamic objects and can concentrate on other parts of the model. We never see any case where the objects still blocked, but there is no way to affirm that blocking never occurs. Finally, the main drawback of this library is the number of messages it generates and by this way, the number of times, the time consuming search of a shortest path is done. However, we think it is possible to ameliorate the whole mechanism, which is the reason of such a detailed presentation.
| THE CLOCK LIBRARY |