 |
ANNEXE - IMPLEMENTATION |
Cet annexe contient des détails sur les implémentations des méthodes présentées dans le mémoire que nous n'avons pas jugés importants de faire apparaître directement dans notre étude. L'objectif de cet annexe est de fournir un supplément d'informations qui peuvent aider dans l'interprétation des résultats, dans leur reproduction et dans l'intégration des divers algorithmes dans un logiciel de conception et/ou de présentation de documents hypermédia synchronisés.
Dans une première partie, nous présentons des algorithmes qui viennent compléter ceux détaillés dans les chapitres précédents. Ensuite, nous expliquons les méthodes que nous avons utilisées pour générer nos instances de problèmes de flot et de tension. Nous présentons également très brièvement les structures de données employées pour représenter les différents éléments manipulés dans nos algorithmes: graphe, cycle, cocycle... Nous terminons enfin par quelques paragraphes sur la manière dont ont été menés les tests: la machine, le système d'exploitation, le compilateur, le nombre d'instances...
| 9.1. ALGORITHMES |
| 9.1.1. Arbre recouvrant |
L'algorithme présenté ici construit un arbre recouvrant d'un graphe
![]() . L'arbre est obtenu sous la forme d'une fonction
. L'arbre est obtenu sous la forme d'une fonction
![]() qui associe à un noeud
qui associe à un noeud
![]() l'arc
l'arc
![]() qui le connecte au reste de l'arbre. Pour établir cette fonction, l'algorithme parcours le
graphe, en partant d'un noeud quelconque et en employant les arcs indifféremment dans le
sens direct ou indirect, et
qui le connecte au reste de l'arbre. Pour établir cette fonction, l'algorithme parcours le
graphe, en partant d'un noeud quelconque et en employant les arcs indifféremment dans le
sens direct ou indirect, et
![]() si
si
![]() est le premier arc qui a permis de visiter
est le premier arc qui a permis de visiter
![]() . Cette méthode étant un simple parcours de graphe, elle nécessite
. Cette méthode étant un simple parcours de graphe, elle nécessite
![]() opérations.
opérations.
pour tout
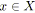 faire
faire
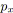

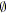 ;
;
soit
 un noeud de
un noeud de
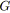 ;
;
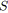

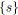 ;
;
tant que
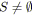 faire
faire
soit
 un noeud de
un noeud de
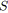 ;
;
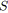

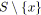 ;
;
pour tout
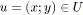 faire
faire
si
 et
et
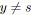 alors
alors


 ;
; 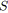

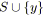 ;
;
fin pour;
pour tout
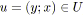 faire
faire
si
 et
et
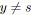 alors
alors


 ;
; 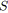

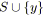 ;
;
fin pour;
fin tant que;
| 9.1.2. Base de cycles |
Cet algorithme permet de construire une base de cycles
![]() pour un graphe
pour un graphe
![]() . Sa justification et son fonctionnement sont présentés à la
section 2.2.1. La méthode repose sur la manipulation d'un arbre recouvrant
. Sa justification et son fonctionnement sont présentés à la
section 2.2.1. La méthode repose sur la manipulation d'un arbre recouvrant
![]() . En lui ajoutant un par un les arcs de
. En lui ajoutant un par un les arcs de
![]() , cela introduit à chaque fois un cycle qui est alors inséré
à la base
, cela introduit à chaque fois un cycle qui est alors inséré
à la base
![]() . Cette méthode nécessite
. Cette méthode nécessite
![]() opérations, il y a
opérations, il y a
![]() arcs à ajouter et chaque fois une détection du cycle ainsi
créé est nécessaire, ce qui s'effectue au pire en
arcs à ajouter et chaque fois une détection du cycle ainsi
créé est nécessaire, ce qui s'effectue au pire en
![]() opérations (puisqu'il y a
opérations (puisqu'il y a
![]() arcs dans l'arbre).
arcs dans l'arbre).
trouver un arbre recouvrant
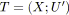 défini par la fonction
défini par la fonction
 ;
;
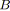

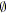 ;
;
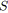

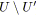 ;
;
tant que
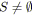 faire
faire
pour tout
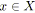 faire
faire
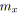
 faux;
faux;
/* Marque pour trouver le cycle. */
soit
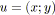 un arc de
un arc de
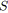 ;
;
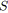

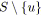 ;
;


 ;
;
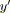

 ;
;
tant que
 faire
faire
soit
 tel que
tel que
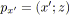 ou
ou
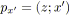 ;
;
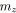
 vrai;
vrai;


 ;
;
fin tant que;
tant que non
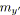 faire
faire
soit
 tel que
tel que
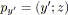 ou
ou
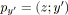 ;
;
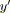

 ;
;
fin tant;
soit le cycle
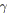 formé des chaînes de
formé des chaînes de
 à
à
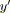 ,
,
de
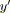 à
à
 et de l'arc
et de l'arc
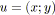 ;
;
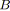

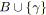 ;
;
fin tant que;
| 9.1.3. Plus court chemin |
Nous rappelons ici l'algorithme dont l'idée générale a été
proposée par L.R. Ford en 1956 pour la recherche d'un plus court chemin entre un noeud
![]() et tous les autres noeuds dans un graphe
et tous les autres noeuds dans un graphe
![]() . Les longueurs
. Les longueurs
![]() des arcs
des arcs
![]() peuvent être négatives et des circuits peuvent exister dans le graphe. La
procédure consiste à repérer un arc
peuvent être négatives et des circuits peuvent exister dans le graphe. La
procédure consiste à repérer un arc
![]() qui ne satisfait pas les conditions d'optimalité du plus court chemin (cf.
section 3.2.4) et à modifier le potentiel de l'une de ses extrémités pour
vérifier la condition, cette opération est répétée
jusqu'à ne plus détecter aucun arc. Cette idée a été reprise par
R.E. Bellman en 1958 (cf. [Bellman58]) en proposant un ordre pour
traiter les arcs qui réduit la complexité de la méthode à
qui ne satisfait pas les conditions d'optimalité du plus court chemin (cf.
section 3.2.4) et à modifier le potentiel de l'une de ses extrémités pour
vérifier la condition, cette opération est répétée
jusqu'à ne plus détecter aucun arc. Cette idée a été reprise par
R.E. Bellman en 1958 (cf. [Bellman58]) en proposant un ordre pour
traiter les arcs qui réduit la complexité de la méthode à
![]() opérations. Elle est toujours la meilleure complexité fortement
polynômiale à ce jour. Cette méthode permet également de détecter
la présence d'un circuit de longueur négative (dont la somme des longueurs des arcs
est négative): lorsqu'un noeud possède un potentiel inférieur à
opérations. Elle est toujours la meilleure complexité fortement
polynômiale à ce jour. Cette méthode permet également de détecter
la présence d'un circuit de longueur négative (dont la somme des longueurs des arcs
est négative): lorsqu'un noeud possède un potentiel inférieur à
![]() (
(![]() étant la longueur maximale d'un arc). Dans l'algorithme que nous
proposons, les plus courts chemins sont obtenus sous la forme d'une fonction
étant la longueur maximale d'un arc). Dans l'algorithme que nous
proposons, les plus courts chemins sont obtenus sous la forme d'une fonction
![]() qui associe à un noeud
qui associe à un noeud
![]() l'arc
l'arc
![]() par lequel le plus court chemin de
par lequel le plus court chemin de
![]() arrive.
arrive.
pour tout
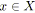 faire
faire
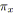

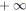 ; /* Le potentiel du noeud. */
; /* Le potentiel du noeud. */
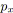

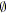 ;
;
fin pour;
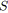

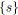 ;
;


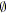 ;
;
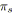

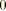 ;
;
tant que
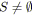 ou
ou
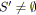 faire
faire
si
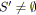 alors
alors
sortir un noeud
 de
de
 ; /* Gestion FIFO de l'ensemble. */
; /* Gestion FIFO de l'ensemble. */
sinon sortir un noeud
 de
de
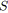 ; /* Gestion FIFO de l'ensemble. */
; /* Gestion FIFO de l'ensemble. */
pour tout
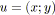 faire
faire
si
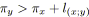 alors
alors
si
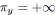 alors
alors
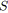

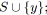
sinon


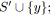
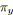

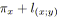 ;
;
si
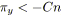 alors /* Circuit de longueur négative. */
alors /* Circuit de longueur négative. */


 ;
;
fin si;
fin pour;
fin tant que;
| 9.1.4. Tri topologique |
Considérons un graphe
![]() sans cycle, avec un seul noeud source. Le tri topologique des noeuds d'un tel graphe
consiste à les ordonner de sorte qu'un noeud est toujours après tous ses
prédécesseurs. L'algorithme proposé ici est un simple parcours des noeuds du
graphe, en partant de sa source
sans cycle, avec un seul noeud source. Le tri topologique des noeuds d'un tel graphe
consiste à les ordonner de sorte qu'un noeud est toujours après tous ses
prédécesseurs. L'algorithme proposé ici est un simple parcours des noeuds du
graphe, en partant de sa source
![]() . Les noeuds sont numérotés dans l'ordre dans lequel ils sont parcourus,
un noeud n'étant visité qu'après tous ses prédécesseurs, ce qui
correspond bien à un ordre topologique. Cette méthode n'étant qu'un simple
parcours, elle nécessite
. Les noeuds sont numérotés dans l'ordre dans lequel ils sont parcourus,
un noeud n'étant visité qu'après tous ses prédécesseurs, ce qui
correspond bien à un ordre topologique. Cette méthode n'étant qu'un simple
parcours, elle nécessite
![]() opérations.
opérations.
pour tout
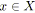 faire
faire
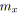

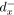 ; /* Marque pour le parcours
topologique. */
; /* Marque pour le parcours
topologique. */
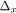

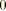 ; /* Numéro dans l'ordre
topologique. */
; /* Numéro dans l'ordre
topologique. */
fin pour;
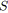

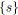 ;
;
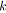

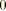 ;
;
tant que
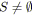 faire
faire
choisir
 dans
dans
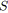 ;
;
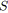

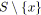 ;
;
pour tout
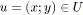 faire
faire
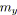

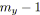 ;
;
si
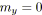 alors
alors
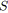

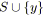 ;
;
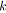

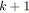 ;
;
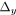

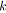 ;
;
fin pour;
fin si;
fin tant que;
| 9.2. GENERATION ALEATOIRE DE PROBLEMES |
La génération de problèmes pour nos jeux d'essais a posé deux difficultés, la première concerne la structure même des graphes, il a fallu créer des graphes connexes (la non connexité ne pose aucune difficulté pour les problèmes que l'on traite, mais nécessite de détecter les composantes connexes et de lancer les méthodes de résolution sur chacune). Il peut être intéressant aussi de générer des graphes sans circuit. Nous avons également généré des graphes série-parallèles et presque série-parallèles. La seconde difficulté consiste à créer les données mêmes du problème, c'est-à-dire les capacités de flot ou de tension selon le problème.
| 9.2.1. Graphes connexes |
Pour générer des graphes connexes avec
![]() noeuds et
noeuds et
![]() arcs, nous avons choisi de créer aléatoirement tout d'abord un arbre
connectant les
arcs, nous avons choisi de créer aléatoirement tout d'abord un arbre
connectant les
![]() noeuds du graphe. Ensuite,
noeuds du graphe. Ensuite,
![]() arcs sont ajoutés au hasard pour compléter le graphe. Lorsqu'un arc est
inséré dans la deuxième phase, il faut éventuellement vérifier
qu'il n'introduit pas de circuit, si c'est le cas il faut alors générer au hasard un
autre arc. Pour créer l'arbre, la procédure consiste à ajouter l'un
après l'autre les noeuds dans le graphe, en les connectant à chaque fois par un arc
avec un noeud déjà présent dans le graphe choisi au hasard.
arcs sont ajoutés au hasard pour compléter le graphe. Lorsqu'un arc est
inséré dans la deuxième phase, il faut éventuellement vérifier
qu'il n'introduit pas de circuit, si c'est le cas il faut alors générer au hasard un
autre arc. Pour créer l'arbre, la procédure consiste à ajouter l'un
après l'autre les noeuds dans le graphe, en les connectant à chaque fois par un arc
avec un noeud déjà présent dans le graphe choisi au hasard.
| 9.2.2. Graphes série-parallèles ou presque |
La génération de graphes série-parallèles est simple. Elle repose
sur la définition même de cette classe de graphes (cf. section 5.1.1). Le graphe se
réduit au départ à un seul arc, ensuite à chaque itération, un
arc du graphe est sélectionné au hasard pour être dédoublé, soit
par une opération série, soit par une opération parallèle. Mais chaque
opération série ajoute un nouveau noeud et un nouvel arc, alors que chaque
opération parallèle ajoute seulement un arc. Cela signifie qu'il faut s'assurer qu'il
y a exactement
![]() opérations séries d'ajoutées dans le graphe et
opérations séries d'ajoutées dans le graphe et
![]() opérations parallèles. Il y a plusieurs possibilités pour
contrôler ces quotas. Nous avons choisi d'appliquer au hasard, mais uniformément, soit
une opération série, soit une opération parallèle quand cela est
possible. Une opération série n'est ajoutée que si le nombre de noeuds limite
n'a pas été atteint, et une opération parallèle n'est appliquée
que si le nombre de noeuds restants à ajouter est inférieur strictement au nombre
d'arcs restants.
opérations parallèles. Il y a plusieurs possibilités pour
contrôler ces quotas. Nous avons choisi d'appliquer au hasard, mais uniformément, soit
une opération série, soit une opération parallèle quand cela est
possible. Une opération série n'est ajoutée que si le nombre de noeuds limite
n'a pas été atteint, et une opération parallèle n'est appliquée
que si le nombre de noeuds restants à ajouter est inférieur strictement au nombre
d'arcs restants.
Générer un graphe presque série-parallèle est très simple. A partir d'un SP-graphe, il suffit d'ajouter au hasard autant d'arcs que nécessaire pour compléter le graphe. Nous verrons pour la génération des problèmes de tension qu'il peut être possible de choisir d'inverser le sens d'un arc au moment où il est inséré, pour se rapprocher des problèmes de synchronisation hypermédia qui ne manipulent que des tensions positives.
| 9.2.3. Problèmes de flot |
Nous proposons ici une méthode pour générer des problèmes dits de flot compatible qui peuvent être étendus très simplement à des problèmes de flot maximal ou de flot de coût minimal.
Soit
![]() et
et
![]() deux fonctions qui associent une valeur (réelle ou entière) à
chaque arc
deux fonctions qui associent une valeur (réelle ou entière) à
chaque arc
![]() du graphe
du graphe
![]() telles que
telles que
![]() .
.
![]() et
et
![]() sont les valeurs minimales et maximales du flot qui peut traverser l'arc
sont les valeurs minimales et maximales du flot qui peut traverser l'arc
![]() . Le problème du flot compatible est de trouver un flot
. Le problème du flot compatible est de trouver un flot
![]() sur
sur
![]() tel que
tel que
![]() .
.
On s'intéresse ici à générer un graphe avec des valeurs de flot minimales et maximales sur les arcs telles qu'il existe au moins un flot compatible. Pour cela, on s'appuie sur la preuve de la section 2.2.1.3 qui permet d'affirmer le corollaire suivant. Tout flot sur un graphe est déterminé par ses seules composantes sur les arcs qui ne sont pas sur un arbre recouvrant donné.
Autrement dit, si on veut générer aléatoirement un flot sur un graphe
![]() , il suffit de trouver un arbre recouvrant de
, il suffit de trouver un arbre recouvrant de
![]() et de tirer totalement au hasard des valeurs de flot pour les arcs qui ne font pas
partie de l'arbre. Ensuite, il faut déterminer les valeurs de flot pour les arcs de l'arbre
afin d'obtenir la conservation des flots. Pour cela nous proposons la méthode suivante.
et de tirer totalement au hasard des valeurs de flot pour les arcs qui ne font pas
partie de l'arbre. Ensuite, il faut déterminer les valeurs de flot pour les arcs de l'arbre
afin d'obtenir la conservation des flots. Pour cela nous proposons la méthode suivante.
On choisit un noeud
![]() de l'arbre
de l'arbre
![]() qui n'a pas de successeur. On cherche à déterminer le flot
qui n'a pas de successeur. On cherche à déterminer le flot
![]() de l'arc
de l'arc
![]() qui le connecte au reste de l'arbre. Pour cela on calcule la valeur suivante.
qui le connecte au reste de l'arbre. Pour cela on calcule la valeur suivante.
Pour garantir la conservation des flots sur le noeud, il suffit de poser
![]() . Ensuite on retire le noeud
. Ensuite on retire le noeud
![]() et l'arc
et l'arc
![]() de l'arbre
de l'arbre
![]() et on recommence avec un autre noeud. On constate à chaque itération que
l'on fixe le flot d'un arc. On obtient finalement bien un flot. Il suffit ensuite de tirer au
hasard un intervalle
et on recommence avec un autre noeud. On constate à chaque itération que
l'on fixe le flot d'un arc. On obtient finalement bien un flot. Il suffit ensuite de tirer au
hasard un intervalle
![]() pour chaque arc
pour chaque arc
![]() autour du flot généré et on obtient un graphe qui admet au moins un flot
compatible.
autour du flot généré et on obtient un graphe qui admet au moins un flot
compatible.
| 9.2.4. Problèmes de tension |
De manière similaire au flot, nous proposons une méthode pour générer des problèmes de tension compatible qui peuvent être étendus très simplement à des problèmes de tension maximale ou de tension de coût minimal.
Soit
![]() et
et
![]() deux fonctions qui associent une valeur (réelle ou entière) à
chaque arc
deux fonctions qui associent une valeur (réelle ou entière) à
chaque arc
![]() du graphe
du graphe
![]() telles que
telles que
![]() .
.
![]() et
et
![]() sont les valeurs minimales et maximales de la tension de l'arc
sont les valeurs minimales et maximales de la tension de l'arc
![]() . Nous rappelons que le problème de la tension compatible est de trouver une
tension
. Nous rappelons que le problème de la tension compatible est de trouver une
tension
![]() sur
sur
![]() telle que
telle que
![]() .
.
On s'intéresse ici à générer un graphe avec des valeurs de tension
minimales et maximales sur les arcs telles qu'il existe au moins une tension compatible. Pour cela,
il suffit de tirer au hasard un potentiel pour chaque noeud du graphe. Ensuite, il faut calculer la
tension des arcs du graphe à l'aide de la définition 2.5. On obtient bien ainsi une
tension. Il suffit alors de tirer au hasard un intervalle
![]() pour chaque arc
pour chaque arc
![]() autour de la tension générée et on obtient un graphe qui admet au moins une
tension compatible.
autour de la tension générée et on obtient un graphe qui admet au moins une
tension compatible.
Il faut noter que jusqu'à présent, aucune contrainte n'a été imposée au signe de la tension. Avec la synchronisation hypermédia, la tension de tout arc doit être positive. La méthode de génération présentée ici ne garantit pas pour les instances qu'il existe une tension compatible positive. Pour cette raison, la méthode de génération aléatoire est légèrement modifiée pour les problèmes de synchronisation hypermédia. Au moment du calcul de la tension d'un arc, si celle-ci s'avère négative, alors l'arc est inversé, i.e. la source devient la destination et vice-versa.
Pour les graphes presque série-parallèles, nous avons opté pour une approche légèrement différente. En effet, une fois le graphe série-parallèle généré, il est possible de le parcourir à partir de la source et d'attribuer un potentiel de plus en plus important à mesure de l'avancée dans le parcours (qui doit être bien sûr topologique). Dans une deuxième phase, des arcs perturbateurs sont ajoutés pour rendre le graphe presque série-parallèle. Pour cela, deux noeuds sont choisis au hasard et un arc est créé entre les deux, si la tension de cet arc est négative, il faut inverser ses extrémités.
| 9.3. STRUCTURES DE DONNEES |
Une seule structure de données a été utilisée pour représenter les graphes dans les différents algorithmes implémentés. La modélisation objet est résumée dans la section 8.1. L'approche choisie est une liste d'adjacence. Un graphe est donc composé d'une liste d'arcs et d'une liste de noeuds. Chaque noeud possède une liste de ses arcs entrants et une liste de ses arcs sortants. Pour la plupart des algorithmes, la structure même de la liste a peu d'importance, car les procédures correspondent principalement à des parcours de ces listes.
|
||||||||||||||||||||||||||
| Tableau 9.1: Complexité des opérations sur la structure de graphe. |
Cependant, pour la méthode d'agrégation notamment, il est nécessaire de
retirer des noeuds et des arcs du graphe. A l'inverse, la méthode de reconstruction par
exemple ajoute des noeuds et des arcs. Il est indispensable que ces opérations s'effectuent
de manière efficace. Malheureusement, il est impossible de garantir une complexité
![]() pour toutes ces opérations à la fois, nous avons donc choisi une
structure qui propose la même complexité pour toutes les opérations. Les listes
sont modélisées sous la forme d'arbres binaires de recherche (la classe
pour toutes ces opérations à la fois, nous avons donc choisi une
structure qui propose la même complexité pour toutes les opérations. Les listes
sont modélisées sous la forme d'arbres binaires de recherche (la classe
map en C++), la clé étant l'identifiant des éléments
stockés. Toutes les opérations dans une map sont en
![]() opérations (
opérations (![]() étant le nombre d'éléments de la structure).
Seul le parcours de tous les éléments nécessite
étant le nombre d'éléments de la structure).
Seul le parcours de tous les éléments nécessite
![]() opérations. Le tableau 9.1 résume la complexité de chaque
opération, il faut juste noter que l'accès aux éléments par leur
clé est à éviter, il est possible d'obtenir un accès en
opérations. Le tableau 9.1 résume la complexité de chaque
opération, il faut juste noter que l'accès aux éléments par leur
clé est à éviter, il est possible d'obtenir un accès en
![]() par leur référence. L'accès par clé est normalement
très rare.
par leur référence. L'accès par clé est normalement
très rare.
Très souvent, les algorithmes nécessitent de manipuler des ensembles de noeuds ou
d'arcs. Nous avons choisi comme structure de données le vecteur (la classe
vector en C++). Elle garantit un accès à un élément en
![]() opérations, un parcours en
opérations, un parcours en
![]() (
(![]() étant le nombre d'éléments), et un ajout et une
suppression en fin de liste en
étant le nombre d'éléments), et un ajout et une
suppression en fin de liste en
![]() opérations. Quand il est nécessaire de gérer une politique
opérations. Quand il est nécessaire de gérer une politique
![]() (First In, First Out), une file d'attente est utilisée (la classe
(First In, First Out), une file d'attente est utilisée (la classe
deque en C++) qui garantit les mêmes complexités que le vecteur avec en
plus un ajout et une suppression en tête de liste en
![]() opérations.
opérations.
Il faut noter que ces structures, vector et deque, reposent sur la
structure de tableau, elles réallouent automatiquement de la mémoire si
nécessaire, ce qui peut conduire dans certaines utilisations à une perte de
performance d'environ
![]() . Lorsque les ensembles manipulés sont triés, nous avons choisi
d'utiliser la structure de
. Lorsque les ensembles manipulés sont triés, nous avons choisi
d'utiliser la structure de map, qui permet un accès en
![]() au premier élément, toutes les autres opérations étant en
au premier élément, toutes les autres opérations étant en
![]() (
(![]() étant le nombre d'éléments).
étant le nombre d'éléments).
| 9.4. RESULTATS NUMERIQUES |
Voici quelques détails supplémentaires sur les expérimentations
menées. Les programmes ont été écrits en C++ et compilés avec
GNU Compiler Collection (GCC) 2.95.3, sous le système d'exploitation Unix AIX 4, avec une
machine RISC-6000 à 160 MHz. L'option de compilation -O3 a été
utilisée pour optimiser la vitesse des programmes.
Les expérimentations ont été menées sur des graphes
générés aléatoirement avec les méthodes présentées
précédemment. Pour prélever les résultats numériques,
![]() instances de chaque problème avec les mêmes caractéristiques ont
été générées. Les résultats présentés dans
le mémoire sont donc des moyennes des données ainsi obtenues, ce qui atténue
l'influence d'une instance particulière sur les résultats.
instances de chaque problème avec les mêmes caractéristiques ont
été générées. Les résultats présentés dans
le mémoire sont donc des moyennes des données ainsi obtenues, ce qui atténue
l'influence d'une instance particulière sur les résultats.
|