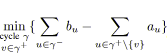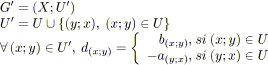|
3. TENSION COMPATIBLE |
| Avant-propos |
Le flot et la tension sont des composantes fortement couplées dans les problèmes de graphes. Cependant, alors que beaucoup d'attention est portée au flot, peu de travaux semblent s'intéresser aux problèmes de tension. Le flot permet en effet de modéliser de nombreux problèmes liés aux flux: télécommunication, transport de marchandises / de personnes... La tension est une notion beaucoup moins naturelle, mais permet néanmoins de modéliser quelques problèmes, plutôt liés à la planification de projets, au placement de dispositifs... (e.g. [Hadjiat96]). En outre, les méthodes d'optimisation de flot reposent très souvent sur un couplage des composantes flot et tension. Nous verrons au cours de notre étude que le flot joue le même rôle dans les problèmes de tension que la tension dans les problèmes de flot.
Dans la première partie, nous avons vu que les principaux problèmes de synchronisation hypermédia peuvent être modélisés comme des problèmes de tension, et plus précisément comme des problèmes de tension compatible et de tension de coût minimal. Nous allons donc tenter dans cette seconde partie de proposer différents algorithmes pour résoudre ces problèmes, discutant des avantages et défauts éventuels de chacun. Il ne faut pas perdre de vue que les méthodes que nous proposons doivent être rapides et ne doivent pratiquement pas dépasser la seconde pour permettre une réponse quasiment en temps réel.
Cet aspect est très important puisqu'il limite notre champs d'investigation. En effet, les graphes traités en synchronisation hypermédia sont relativement petits et ne dépassent pas à l'heure actuelle la centaine de noeuds. Il est alors impossible d'employer des algorithmes qui ont une bonne complexité théorique, mais qui révèlent leur efficacité sur des graphes de grande taille. Des algorithmes considérés moins efficaces en théorie peuvent tout à fait convenir, et s'avérer plus efficaces, sur des graphes de petite taille.
Les auteurs de documents hypermédia affirment actuellement qu'une centaine de noeuds
suffit amplement pour les documents qu'ils souhaitent créer. Mais il est très
difficile, même pour des experts, d'envisager les besoins et les possibilités futures,
l'histoire de l'informatique est remplie d'exemples dans ce sens (le plus célèbre
étant la phrase "640 Ko of RAM is enough"). Il est donc raisonnable de
penser que si des outils efficaces de synchronisation hypermédia se répandent, la
taille des documents manipulés augmentera et dépassera largement les besoins actuels.
Il en existe déjà un exemple présenté dans [Vazirgiannis98] qui tente de synchroniser
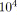 objets dans un film
de synthèse de 90 minutes. Il est donc important de s'intéresser tout de même
au comportement théorique et pratique de nos algorithmes sur des graphes de taille
conséquente.
objets dans un film
de synthèse de 90 minutes. Il est donc important de s'intéresser tout de même
au comportement théorique et pratique de nos algorithmes sur des graphes de taille
conséquente.
Dans les deux premiers chapitres de cette seconde partie, nous nous intéressons aux problèmes de la tension compatible et de la tension minimale sur des graphes quelconques. Cependant, il est facile de s'apercevoir, en regardant notamment les relations d'Allen, que des graphes temporels issus d'une synchronisation hypermédia sont très organisés. Une classe de graphes semble très proche de cette structure: les graphes série-parallèles. Nous consacrons donc un dernier chapitre à l'étude du problème de tension de coût minimal sur cette classe de graphes. Cependant, les graphes issus d'une synchronisation hypermédia sont légèrement moins structurés que les graphes série-parallèles. Nous proposons une approche qui permet d'optimiser la tension d'un graphe presque série-parallèle en profitant tout de même de sa structure série-parallèle.
| INTRODUCTION |
Avant de chercher à optimiser une tension dans un graphe, il faut déjà
être capable de trouver efficacement une tension compatible. Nous rappelons tout
d'abord ce problème, il s'agit de trouver une tension
![]() sur un graphe
sur un graphe
![]() , avec
, avec
![]() et
et
![]() , telle que pour tout arc
, telle que pour tout arc
![]() ,
,
![]() , où
, où
![]() et
et
![]() sont des valeurs réelles ou entières. Dans sa thèse, M. Hadjiat
(cf. [Hadjiat96]) propose deux manières de résoudre ce
problème. En fait, les algorithmes reposent sur deux façons différentes de
trouver la tension maximale pour un arc donné, l'une se base sur des plus courts chemins,
l'autre sur la recherche de cocycles. Nous proposons ici de réviser ces approches en
abordant directement le problème de la tension compatible.
sont des valeurs réelles ou entières. Dans sa thèse, M. Hadjiat
(cf. [Hadjiat96]) propose deux manières de résoudre ce
problème. En fait, les algorithmes reposent sur deux façons différentes de
trouver la tension maximale pour un arc donné, l'une se base sur des plus courts chemins,
l'autre sur la recherche de cocycles. Nous proposons ici de réviser ces approches en
abordant directement le problème de la tension compatible.
| 3.1. RECHERCHE D'UNE TENSION MAXIMALE SUR UN ARC |
Nous nous intéressons tout d'abord au problème de la tension maximale.
Soit un arc
![]() donné du graphe
donné du graphe
![]() , il faut trouver la valeur maximale de la tension
, il faut trouver la valeur maximale de la tension
![]() de l'arc, sachant que
de l'arc, sachant que
![]() doit être compatible. En d'autres termes, nous cherchons:
doit être compatible. En d'autres termes, nous cherchons:
| 3.1.1. Algorithme basé sur le plus court chemin |
Nous rappelons ici l'algorithme proposé dans [Hadjiat96]. Il
implique plusieurs propriétés très intéressantes et utiles pour la
suite. Soit
![]() une tension compatible. Pour tout cycle
une tension compatible. Pour tout cycle
![]() , on a
, on a
![]() . Donc, pour tout cycle
. Donc, pour tout cycle
![]() contenant l'arc
contenant l'arc
![]() , on peut affirmer (en prenant comme sens de parcours du cycle le sens de l'arc
, on peut affirmer (en prenant comme sens de parcours du cycle le sens de l'arc
![]() ):
):
D'où la proposition suivante.
Pour toute tension compatible et pour tout cycle
contenant l'arc
tel que
, on a:
(3.1)
La tension maximale de l'arc
![]() est donc bornée par:
est donc bornée par:
L'algorithme 3.2 présenté dans la section 3.1.2 démontre que cette borne est accessible, d'où la proposition suivante (une démonstration non constructive peut également être trouvée dans [Berge62]).
La tension maximale d'un arc est égale à:
(3.2)
Considérons un cycle
![]() contenant
contenant
![]() . Il est possible de former une chaîne
. Il est possible de former une chaîne
![]() de
de
![]() à
à
![]() telle que
telle que
![]() . Autrement dit,
. Autrement dit,
![]() est la chaîne formée en enlevant
est la chaîne formée en enlevant
![]() du cycle
du cycle
![]() . Appelons capacité de
. Appelons capacité de
![]() la valeur
la valeur
![]() (attention, dans la chaîne les arcs sont dans le sens opposé à
celui qu'ils ont dans le cycle). Ainsi, la proposition 3.2 peut s'énoncer de la
manière suivante.
(attention, dans la chaîne les arcs sont dans le sens opposé à
celui qu'ils ont dans le cycle). Ainsi, la proposition 3.2 peut s'énoncer de la
manière suivante.
La tension maximale sur l'arc est égale à la capacité minimale des chaînes allant de
à
.
(3.3)
Trouver la tension maximale d'un arc consiste donc à trouver une chaîne de
capacité minimale entre
![]() et
et
![]() . L'idée ici est de transformer le graphe
. L'idée ici est de transformer le graphe
![]() en un graphe
en un graphe
![]() de manière à ce que la recherche d'une chaîne de capacité
minimale dans
de manière à ce que la recherche d'une chaîne de capacité
minimale dans
![]() se traduise par une recherche d'un plus court chemin dans
se traduise par une recherche d'un plus court chemin dans
![]() pour laquelle de nombreux algorithmes existent déjà. La transformation
est illustrée par la figure 3.1. Il s'agit de dédoubler chaque arc
pour laquelle de nombreux algorithmes existent déjà. La transformation
est illustrée par la figure 3.1. Il s'agit de dédoubler chaque arc
![]() en deux arcs
en deux arcs
![]() et
et
![]() où
où
![]() porte la distance
porte la distance
![]() et
et
![]() la distance
la distance
![]() .
.
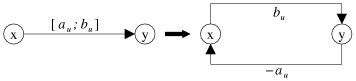 |
| Figure 3.1: Transformation d'une chaîne maximale en un plus court chemin. |
En résumé,
![]() se construit de la manière suivante,
se construit de la manière suivante,
![]() étant la fonction de distance sur les arcs.
étant la fonction de distance sur les arcs.
Certaines distances dans
![]() sont négatives. Il serait donc possible de rencontrer des circuits de longueur
négative, i.e. la somme des distances des arcs sur le cycle serait négative. Il
serait alors impossible de déterminer un plus court chemin. Dans notre cas, nous pouvons
démontrer la proposition suivante.
sont négatives. Il serait donc possible de rencontrer des circuits de longueur
négative, i.e. la somme des distances des arcs sur le cycle serait négative. Il
serait alors impossible de déterminer un plus court chemin. Dans notre cas, nous pouvons
démontrer la proposition suivante.
Il existe une tension compatible sur le graphe si et seulement si:
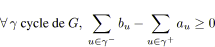
(3.4)
Preuve:
(![]() ) Soit
) Soit
![]() une tension compatible. D'après la proposition 3.1, pour tout cycle
une tension compatible. D'après la proposition 3.1, pour tout cycle
![]() de
de
![]() et un arc
et un arc
![]() , on a:
, on a:
![]() . Comme
. Comme
![]() est compatible, on a
est compatible, on a
![]() . D'où
. D'où
![]() , donc
, donc
![]() .
.
(![]() ) Supposons qu'il n'existe pas de tension compatible. En utilisant la définition
de la tension à partir de la matrice d'incidence
) Supposons qu'il n'existe pas de tension compatible. En utilisant la définition
de la tension à partir de la matrice d'incidence
![]() et du potentiel
et du potentiel
![]() , cela signifie que le système suivant n'a pas de solution.
, cela signifie que le système suivant n'a pas de solution.
![]()
D'après le théorème de Fourier-Motzkin (cf. [Mangasarian69]), un système linéaire n'a pas de solution si et
seulement s'il existe une dépendance linéaire des équations du système
donnant une conséquence fausse (i.e. une relation linéaire des équations qui
ne peut jamais être satisfaite). Pour notre système
![]() , cela signifie qu'il existe un flot
, cela signifie qu'il existe un flot
![]() et deux vecteurs
et deux vecteurs
![]() et
et
![]() tels que
tels que
![]() et
et
![]() . En utilisant la décomposition d'un flot sur une base de cycles
. En utilisant la décomposition d'un flot sur une base de cycles
![]() , il existe donc un cycle
, il existe donc un cycle
![]() de
de
![]() tel que
tel que
![]() .
.
![]()
La détection d'un cycle négatif lors de la recherche d'un plus court chemin
indique alors qu'il n'existe pas de tension compatible dans le graphe
![]() . Pour déterminer la tension maximale d'un arc, M. Hadjiat propose donc
l'algorithme 3.1.
. Pour déterminer la tension maximale d'un arc, M. Hadjiat propose donc
l'algorithme 3.1.
Algorithme 3.1: tensionMaximaleChemin(arc,
graphe,réel
)
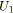

;
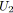

;
pour toutfaire
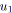

;
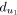

;
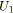

;
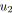

;
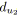

;
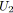

;
fin pour;
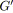

;
plusCourtChemin(,
,
,
,
); /* Au retour
est un plus court chemin. */
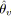
longueur(
);
fin algorithme;
Cette procédure nécessite un algorithme de plus court chemin qui manipule des
longueurs négatives et prend en compte les circuits, ce qui exclut les algorithmes de
label-setting (cf. [Ahuja93]) comme celui de Bellman (à
cause des circuits) et celui de Dijkstra (à cause des valeurs négatives). Dans
[Hadjiat96], M. Hadjiat opte donc pour un algorithme de
label-correcting comme celui de Bellman et Ford qui s'exécute en
![]() opérations (cf. [Ahuja93]) et qui détecte les
cycles négatifs. Cet algorithme peut être trouvé dans l'annexe.
opérations (cf. [Ahuja93]) et qui détecte les
cycles négatifs. Cet algorithme peut être trouvé dans l'annexe.
| 3.1.2. Algorithme basé sur le cocycle augmentant |
L'algorithme présenté ici est extrait de [Hadjiat96].
Il introduit un mécanisme intéressant pour manipuler et modifier une tension.
Considérons un cocycle
![]() qui sépare l'ensemble de noeuds
qui sépare l'ensemble de noeuds
![]() du reste du graphe. Si on diminue de
du reste du graphe. Si on diminue de
![]() la tension des arcs du cocycle dans le sens
la tension des arcs du cocycle dans le sens
![]() vers
vers
![]() et si on augmente de la même valeur
et si on augmente de la même valeur
![]() la tension des arcs du cocycle dans le sens
la tension des arcs du cocycle dans le sens
![]() vers
vers
![]() , les valeurs obtenues définissent toujours une tension. En effet, au niveau des
potentiels, cela revient à augmenter de
, les valeurs obtenues définissent toujours une tension. En effet, au niveau des
potentiels, cela revient à augmenter de
![]() tous les potentiels de
tous les potentiels de
![]() : les tensions des arcs dans le sous-graphe engendré par
: les tensions des arcs dans le sous-graphe engendré par
![]() ne changent pas, seules les tensions sur le cocycle changent. (Notons qu'un
phénomène similaire peut être constaté en modifiant le flot des arcs
d'un cycle
ne changent pas, seules les tensions sur le cocycle changent. (Notons qu'un
phénomène similaire peut être constaté en modifiant le flot des arcs
d'un cycle
![]() : en augmentant par exemple le flot des arcs de
: en augmentant par exemple le flot des arcs de
![]() et en diminuant le flot des arcs de
et en diminuant le flot des arcs de
![]() , la conservation des flots est toujours assurée dans le graphe.)
, la conservation des flots est toujours assurée dans le graphe.)
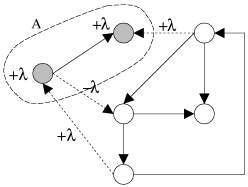 |
| Figure 3.2: Modification de la tension sur un cocycle. |
Ainsi, de manière générale, si l'on veut augmenter la tension d'un arc
![]() , il suffit de rechercher un cocycle pour lequel tous les arcs
, il suffit de rechercher un cocycle pour lequel tous les arcs
![]() du cocycle dans le même sens n'ont pas atteint leur capacité maximale
(i.e.
du cocycle dans le même sens n'ont pas atteint leur capacité maximale
(i.e.
![]() ) et tous les arcs
) et tous les arcs
![]() du cocycle dans le sens opposé n'ont pas atteint leur capacité minimale
(i.e.
du cocycle dans le sens opposé n'ont pas atteint leur capacité minimale
(i.e.
![]() ). [Hadjiat96] propose donc de rechercher un tel cocycle en
utilisant l'algorithme basé sur le lemme de Minty avec la coloration suivante.
). [Hadjiat96] propose donc de rechercher un tel cocycle en
utilisant l'algorithme basé sur le lemme de Minty avec la coloration suivante.
- Tout arc
 tel que
tel que
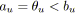 est noir.
est noir.
- Tout arc
 tel que
tel que
 est bleu.
est bleu.
- Tout arc
 tel que
tel que
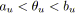 est rouge.
est rouge.
- Tout arc
 tel que
tel que
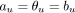 est vert.
est vert.
On s'aperçoit alors que si l'algorithme détecte un cocycle avec cette coloration,
la tension de
![]() peut être augmentée. Si un cycle
peut être augmentée. Si un cycle
![]() est obtenu, alors il vérifie
est obtenu, alors il vérifie
![]() et
et
![]() , ce qui signifie que ce cycle correspond à une chaîne de capacité
minimale pour
, ce qui signifie que ce cycle correspond à une chaîne de capacité
minimale pour
![]() . [Hadjiat96] propose donc l'algorithme 3.2 pour
déterminer une tension maximale pour un arc
. [Hadjiat96] propose donc l'algorithme 3.2 pour
déterminer une tension maximale pour un arc
![]() donné.
donné.
Algorithme 3.2: tensionMaximaleCocycle(tension,arc
,
graphe,réel
)
/* La tensiondoit être compatible. */
colorer les arcs de;
cycleMinty(,
,
,
);
tant que cocyclefaire


;
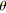

;
colorer les arcs de;
cycleMinty(,
,
,
);
fin tant que;
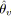

;
fin algorithme;
Après une augmentation de la tension sur un cocycle
![]() , au moins un arc
, au moins un arc
![]() devient saturé, i.e.
devient saturé, i.e.
![]() ou
ou
![]() . Cet arc devient alors noir ou bleu et permet au prochain appel à la recherche
d'un cocycle de marquer un noeud de plus. Ainsi un cycle est détecté au plus en
. Cet arc devient alors noir ou bleu et permet au prochain appel à la recherche
d'un cocycle de marquer un noeud de plus. Ainsi un cycle est détecté au plus en
![]() itérations. La partie principale de l'algorithme s'exécute donc en
itérations. La partie principale de l'algorithme s'exécute donc en
![]() opérations, la partie qui établit une tension compatible n'étant
pas comptée.
opérations, la partie qui établit une tension compatible n'étant
pas comptée.
| 3.2. RECHERCHE D'UNE TENSION COMPATIBLE |
[Hadjiat96] propose deux algorithmes pour trouver une tension compatible qui reposent sur les deux méthodes de recherche de tension maximale exposées précédemment. Nous présentons ici ces deux algorithmes avant de proposer deux variantes qui abordent directement le problème de la tension compatible.
| 3.2.1. Algorithme basé sur le plus court chemin |
Ce premier algorithme repose sur la proposition suivante.
Soit une tension compatible pour laquelle
pour un arc donné
. Si
est la chaîne de capacité minimale reliant les deux extrémités de cet arc, on a:
et
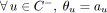
(3.5)
Preuve:
![]() étant compatible,
étant compatible,
![]() . Si
. Si
![]() forme à lui seul la chaîne minimale, la preuve est évidente.
Sinon, on a
forme à lui seul la chaîne minimale, la preuve est évidente.
Sinon, on a
![]() . La soustraction des deux équations entraîne
. La soustraction des deux équations entraîne
![]() .
.
![]() étant compatible, tous les termes de la somme sont positifs ou nuls, et donc
avec l'équation ils ne peuvent être que nuls.
étant compatible, tous les termes de la somme sont positifs ou nuls, et donc
avec l'équation ils ne peuvent être que nuls.
![]()
Cette proposition permet d'affirmer que si l'on restreint l'intervalle de tension sur les arcs
d'une chaîne minimale
![]() à
à
![]() pour tout arc
pour tout arc
![]() et à
et à
![]() pour tout arc
pour tout arc
![]() , alors il existe quand même une tension compatible sur le graphe. D'où
l'algorithme 3.3 qui détecte une chaîne minimale, restreint les intervalles sur la
chaîne et recommence jusqu'à ce que tous les intervalles de tension soient des
singletons.
, alors il existe quand même une tension compatible sur le graphe. D'où
l'algorithme 3.3 qui détecte une chaîne minimale, restreint les intervalles sur la
chaîne et recommence jusqu'à ce que tous les intervalles de tension soient des
singletons.
Algorithme 3.3: tensionCompatibleChemin(graphe
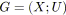 ,tension
,tension
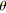 )
)
tant que
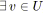 tel que
tel que
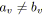 faire
faire
sélectionner un tel arc
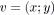 ;
;
trouver chaîne minimale
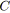 de
de
 à
à
 ; /* Cf. algorithme 3.1. */
; /* Cf. algorithme 3.1. */
pour tout
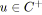 faire
faire
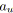

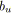 ;
;
pour tout
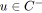 faire
faire
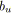

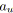 ;
;


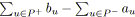 ;
;
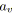

 ;
;
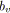

 ;
;
fin tant que;
pour tout
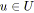 faire
faire
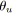

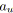 ;
;
fin algorithme; Si un cycle négatif est détecté lors de la première recherche de
chaîne minimale, alors il n'existe pas de tension compatible. A chaque itération, au
moins un intervalle est restreint à un singleton. Ainsi l'algorithme effectue au plus
![]() recherches de chaîne minimale. Il s'exécute donc en
recherches de chaîne minimale. Il s'exécute donc en
![]() opérations.
opérations.
| 3.2.2. Algorithme basé sur le cocycle augmentant |
Voici le second algorithme proposé dans [Hadjiat96]. Soit
![]() une tension quelconque. Considérons un arc
une tension quelconque. Considérons un arc
![]() non compatible. Soit
non compatible. Soit
![]() , soit
, soit
![]() . Dans le premier cas, on va tenter d'augmenter au maximum la tension
. Dans le premier cas, on va tenter d'augmenter au maximum la tension
![]() et dans le second cas, on va tenter de diminuer au maximum
et dans le second cas, on va tenter de diminuer au maximum
![]() .
.
Algorithme 3.4: tensionCompatibleCocycle(graphe
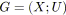 ,tension
,tension
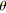 )
)
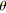
 0;
0;
tant que
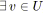 tel que
tel que
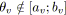 faire
faire
sélectionner un tel arc
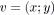 ;
;
/* Modification des capacités pour rendre
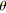 virtuellement compatible. */
virtuellement compatible. */
pour tout
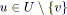 faire
faire
si
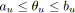 alors
alors
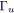

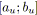 ;
;
sinon si
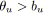 alors
alors
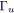

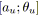 ;
;
sinon
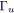

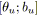 ;
;
fin pour;
si
 alors /* La tension va être maximisée. */
alors /* La tension va être maximisée. */
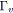

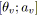 ;
;
tensionMaximaleCocycle(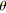 ,
, ,
,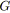 ); /* Avec les intervalles
); /* Avec les intervalles
 . */
. */
si
 alors arrêter; /* Pas de tension compatible. */
alors arrêter; /* Pas de tension compatible. */
sinon /* La tension va être minimisée. */
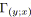

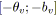 ;
;
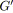

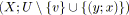 ;
;
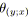

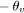 ;
;
tensionMaximaleCocycle(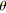 ,
, ,
,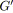 ); /* Avec les intervalles
); /* Avec les intervalles
 . */
. */
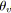

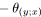 ;
;
si
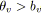 alors arrêter; /* Pas de tension compatible. */
alors arrêter; /* Pas de tension compatible. */
fin si;
fin tant que;
fin algorithme; Pour cela, on utilise l'algorithme 3.2 qui maximise la tension d'un arc. Dans le premier cas,
la méthode est appliquée directement sur
![]() dans le graphe
dans le graphe
![]() . Dans le second cas,
. Dans le second cas,
![]() nécessite une modification: l'arc
nécessite une modification: l'arc
![]() est inversé et ses valeurs de tension sont remplacées par leur
opposé. Ainsi, l'algorithme de maximisation est appliqué sur
est inversé et ses valeurs de tension sont remplacées par leur
opposé. Ainsi, l'algorithme de maximisation est appliqué sur
![]() pour maximiser
pour maximiser
![]() et donc minimiser
et donc minimiser
![]() .
.
La tension sera arbitrairement choisie nulle au début. Cependant, l'algorithme 3.2
suppose une tension
![]() compatible, ce qui est justement le but de l'algorithme présenté ici.
Pour satisfaire à cette hypothèse, une transformation des bornes de tension est
proposée qui rend
compatible, ce qui est justement le but de l'algorithme présenté ici.
Pour satisfaire à cette hypothèse, une transformation des bornes de tension est
proposée qui rend
![]() virtuellement compatible à chaque itération et qui, lors de la
maximisation ou de la minimisation, n'altère pas la compatibilité déjà
acquise par d'autres arcs.
virtuellement compatible à chaque itération et qui, lors de la
maximisation ou de la minimisation, n'altère pas la compatibilité déjà
acquise par d'autres arcs.
A chaque itération, un arc est rendu compatible. Ainsi l'algorithme exécute
![]() fois l'algorithme de maximisation de la tension. L'algorithme s'exécute donc en
fois l'algorithme de maximisation de la tension. L'algorithme s'exécute donc en
![]() opérations.
opérations.
| 3.2.3. Variante de l'algorithme basé sur le cocycle augmentant |
Les algorithmes précédents réduisent le problème de la tension compatible à des problèmes de tension maximale sur un arc, nous proposons ici d'aborder directement le problème de la tension compatible. Mais avant de parler de l'algorithme, nous démontrons la proposition suivante.
Soit un cycle, si
alors les seules tensions compatibles
qui peuvent exister sur le graphe
vérifient
pour tout
et
pour tout
.
(3.6)
Preuve:
D'après la proposition 3.1, pour tout arc
![]() on a:
on a:
![]() . Donc la seule tension compatible pour l'arc
. Donc la seule tension compatible pour l'arc
![]() est
est
![]() . De la même manière, pour tout arc
. De la même manière, pour tout arc
![]() , la seule tension compatible pour l'arc
, la seule tension compatible pour l'arc
![]() est
est
![]() .
.
![]()
L'idée de l'algorithme ici est de considérer une tension quelconque (on peut
choisir la tension nulle) qui n'est généralement pas compatible. Cela signifie que
l'on peut trouver un arc
![]() tel que
tel que
![]() ou
ou
![]() . Dans le premier cas, on cherchera un cocycle qui permet une augmentation de
. Dans le premier cas, on cherchera un cocycle qui permet une augmentation de
![]() . Voici la coloration que nous proposons pour rechercher un tel cocycle.
. Voici la coloration que nous proposons pour rechercher un tel cocycle.
- Tout arc
 tel que
tel que
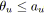 et
et
 est noir.
est noir.
- Tout arc
 tel que
tel que
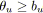 et
et
 est bleu.
est bleu.
- Tout arc
 tel que
tel que
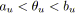 est rouge.
est rouge.
- Tout arc
 tel que
tel que
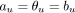 est vert.
est vert.
Avec cette coloration, soit on trouve un cocycle qui permet d'augmenter la tension de
![]() , soit on trouve un cycle, ce qui signifie qu'il n'existe pas de tension compatible.
, soit on trouve un cycle, ce qui signifie qu'il n'existe pas de tension compatible.
Preuve:
Si aucun cocycle n'existe avec cette coloration, alors il existe un cycle
![]() contenant
contenant
![]() .
.
![]() contient des arcs noirs, avec
contient des arcs noirs, avec
![]() , et des arcs verts, avec
, et des arcs verts, avec
![]() , donc tous les arcs de
, donc tous les arcs de
![]() vérifient
vérifient
![]() . De la même manière, les arcs bleus et verts de
. De la même manière, les arcs bleus et verts de
![]() vérifient tous
vérifient tous
![]() . Donc
. Donc
![]() . Ainsi, soit
. Ainsi, soit
![]() , auquel cas il n'existe pas de tension compatible, soit
, auquel cas il n'existe pas de tension compatible, soit
![]() . La proposition 3.6 induit alors que
. La proposition 3.6 induit alors que
![]() , or
, or
![]() pour l'instant et il n'existe pas de cocycle pour augmenter la tension de
pour l'instant et il n'existe pas de cocycle pour augmenter la tension de
![]() . Donc cela signifie qu'il n'existe pas de tension compatible.
. Donc cela signifie qu'il n'existe pas de tension compatible.
![]()
Dans le cas où
![]() , on cherchera un cocycle qui permet une diminution de
, on cherchera un cocycle qui permet une diminution de
![]() . Voici la coloration (notée
. Voici la coloration (notée
![]() ) que nous proposons pour rechercher un tel cocycle. Seulement les couleurs bleu et
noir sont inversées par rapport à la première coloration (notée
) que nous proposons pour rechercher un tel cocycle. Seulement les couleurs bleu et
noir sont inversées par rapport à la première coloration (notée
![]() ).
).
- Tout arc
 tel que
tel que
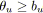 et
et
 est noir.
est noir.
- Tout arc
 tel que
tel que
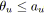 et
et
 est bleu.
est bleu.
- Tout arc
 tel que
tel que
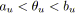 est rouge.
est rouge.
- Tout arc
 tel que
tel que
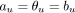 est vert.
est vert.
Avec cette coloration, soit on trouve un cocycle qui permet de diminuer la tension de
![]() , soit on trouve un cycle, ce qui signifie qu'il n'existe pas de tension compatible (la
preuve est similaire à celle du premier cas). Voici donc l'algorithme complet qui permet de
déterminer une tension compatible sur le graphe
, soit on trouve un cycle, ce qui signifie qu'il n'existe pas de tension compatible (la
preuve est similaire à celle du premier cas). Voici donc l'algorithme complet qui permet de
déterminer une tension compatible sur le graphe
![]() .
.
Algorithme 3.5: tensionCompatibleCocycleBis(graphe
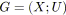 ,tension
,tension
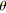 )
)
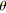
 0;
0;
tant que
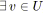 tel que
tel que
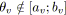 faire
faire
sélectionner un tel arc
 ;
;
si
 alors
alors
cycleMinty( ,
,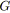 ,
,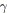 ,
, );
/* Avec la coloration
);
/* Avec la coloration
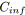 . */
. */
si
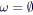 alors arrêter; /* Pas de tension compatible. */
alors arrêter; /* Pas de tension compatible. */


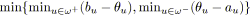 ;
;
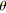

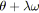 ;
;
sinon
cycleMinty( ,
,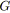 ,
,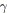 ,
, );
/* Avec la coloration
);
/* Avec la coloration
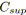 . */
. */
si
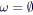 alors arrêter; /* Pas de tension compatible. */
alors arrêter; /* Pas de tension compatible. */


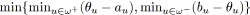 ;
;
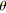

 ;
;
fin si;
fin tant que;
fin algorithme; Si on ne considère pas une méthode particulière de sélection de
l'arc à traiter à chaque itération, l'algorithme s'exécute en
![]() opérations dans le cas où les bornes de tension sont entières et
en
opérations dans le cas où les bornes de tension sont entières et
en
![]() dans le cas où elles sont réelles,
dans le cas où elles sont réelles,
![]() étant la plus grande borne de tension en valeur absolue, i.e.
étant la plus grande borne de tension en valeur absolue, i.e.
![]() , et
, et
![]() une borne inférieure de
une borne inférieure de
![]() pour toute itération de l'algorithme. Une valeur possible de
pour toute itération de l'algorithme. Une valeur possible de
![]() est:
est:
Preuve:
Dans le cas entier, il est évident qu'à chaque itération, la tension de l'arc
![]() est améliorée d'au moins 1. Donc, au maximum en
est améliorée d'au moins 1. Donc, au maximum en
![]() itérations,
itérations,
![]() aura atteint soit
aura atteint soit
![]() , soit
, soit
![]() . L'algorithme appelle donc
. L'algorithme appelle donc
![]() fois l'algorithme de recherche de cocycle.
fois l'algorithme de recherche de cocycle.
Dans le cas réel, on s'aperçoit que la tension d'un arc est toujours une combinaison
linéaire (avec des coefficients entiers) des bornes des intervalles de tension. Autrement
dit, pour tout arc
![]() et à toute itération de l'algorithme, il existe
et à toute itération de l'algorithme, il existe
![]() et
et
![]() tels que
tels que
![]() . C'est très facile à vérifier dans la mesure où toutes les
tensions sont à zéro au départ et qu'à chaque itération la
valeur ajoutée ou retranchée à une tension est une différence entre une
tension et une borne. Cela veut dire que la valeur
. C'est très facile à vérifier dans la mesure où toutes les
tensions sont à zéro au départ et qu'à chaque itération la
valeur ajoutée ou retranchée à une tension est une différence entre une
tension et une borne. Cela veut dire que la valeur
![]() à chaque itération est une combinaison linéaire. La plus petite
valeur de
à chaque itération est une combinaison linéaire. La plus petite
valeur de
![]() s'exprime donc
s'exprime donc
![]() . Cette valeur existe puisque l'ensemble dans lequel est recherché le minimum
est dénombrable et majoré par 0. A chaque itération, la tension de l'arc
. Cette valeur existe puisque l'ensemble dans lequel est recherché le minimum
est dénombrable et majoré par 0. A chaque itération, la tension de l'arc
![]() est améliorée d'au moins
est améliorée d'au moins
![]() . Donc, au maximum en
. Donc, au maximum en
![]() itérations,
itérations,
![]() aura atteint soit
aura atteint soit
![]() , soit
, soit
![]() . L'algorithme appelle ainsi
. L'algorithme appelle ainsi
![]() fois l'algorithme de recherche de cocycle.
fois l'algorithme de recherche de cocycle.
![]()
En revanche, si on choisit dans l'algorithme de sélectionner un arc et de
l'améliorer tant qu'il n'est pas compatible (cf. algorithme 3.6), on se ramène
à l'algorithme 3.4 qui maximise la tension de chaque arc. Dans ce cas, au maximum
![]() opérations sont nécessaires pour rendre un arc compatible (l'algorithme
de recherche de cocycle marque un nouveau noeud à chaque itération), aussi bien dans
le cas réel que dans le cas entier. L'algorithme s'exécute donc dans cette version en
opérations sont nécessaires pour rendre un arc compatible (l'algorithme
de recherche de cocycle marque un nouveau noeud à chaque itération), aussi bien dans
le cas réel que dans le cas entier. L'algorithme s'exécute donc dans cette version en
![]() opérations.
opérations.
Algorithme 3.6: tensionCompatibleCocycle(graphe
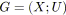 ,tension
,tension
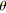 )
)
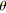
 0;
0;
tant que
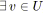 tel que
tel que
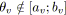 faire
faire
sélectionner un tel arc
 ;
;
tant que
 alors
alors
cycleMinty( ,
,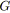 ,
,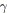 ,
, );
/* Avec la coloration
);
/* Avec la coloration
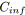 . */
. */
si
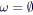 alors arrêter; /* Pas de tension compatible. */
alors arrêter; /* Pas de tension compatible. */


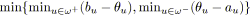 ;
;
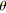

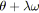 ;
;
fin tant que;
tant que
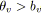 alors
alors
cycleMinty( ,
,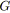 ,
,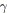 ,
, );
/* Avec la coloration
);
/* Avec la coloration
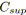 . */
. */
si
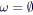 alors arrêter; /* Pas de tension compatible. */
alors arrêter; /* Pas de tension compatible. */


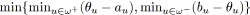 ;
;
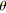

 ;
;
fin tant que;
fin tant que;
fin algorithme;| 3.2.4. Un autre algorithme basé sur le plus court chemin |
Reprenons ici quelques résultats sur les problèmes de plus court chemin
que l'on peut retrouver dans [Ahuja93]. Supposons que l'on cherche la
plus courte distance entre un noeud
![]() et tous les autres noeuds du graphe
et tous les autres noeuds du graphe
![]() . Notons
. Notons
![]() la fonction qui associe à chaque arc
la fonction qui associe à chaque arc
![]() une longueur. Voici les conditions nécessaires et suffisantes, appelées
conditions d'optimalité du plus court chemin, qui prouvent qu'une distance est la
plus courte.
une longueur. Voici les conditions nécessaires et suffisantes, appelées
conditions d'optimalité du plus court chemin, qui prouvent qu'une distance est la
plus courte.
Soit une fonction qui associe une valeur à chaque noeud du graphe
. Si pour tout noeud
,
est la distance d'un chemin de
à
, alors
représente la plus courte distance entre
et
si et seulement si
.
(3.7)
Preuve:
(![]() ) Considérons un arc
) Considérons un arc
![]() . Soit le plus court chemin entre
. Soit le plus court chemin entre
![]() et
et
![]() passe par
passe par
![]() , soit le plus court chemin entre
, soit le plus court chemin entre
![]() et
et
![]() est un chemin
est un chemin
![]() ne contenant pas
ne contenant pas
![]() . Dans le premier cas, la plus courte distance de
. Dans le premier cas, la plus courte distance de
![]() à
à
![]() est
est
![]() qui vaut également
qui vaut également
![]() si on considère de passer par
si on considère de passer par
![]() . La condition d'optimalité est alors vérifiée. Dans le second cas,
le plus court chemin de
. La condition d'optimalité est alors vérifiée. Dans le second cas,
le plus court chemin de
![]() à
à
![]() passant par
passant par
![]() a une longueur de
a une longueur de
![]() qui est forcément supérieure à la longueur du chemin
qui est forcément supérieure à la longueur du chemin
![]() , autrement dit
, autrement dit
![]() . Là aussi, la condition d'optimalité est vérifiée.
. Là aussi, la condition d'optimalité est vérifiée.
(![]() ) Considérons un chemin
) Considérons un chemin
![]() de
de
![]() à un noeud
à un noeud
![]() . Supposons que ce chemin ait une longueur inférieure à
. Supposons que ce chemin ait une longueur inférieure à
![]() . Cela signifie que
. Cela signifie que
![]() . Cependant, les conditions d'optimalité assurent que
. Cependant, les conditions d'optimalité assurent que
![]() . Donc,
. Donc,
![]() . D'où la contradiction.
. D'où la contradiction.
![]()
Une petite remarque: s'il n'existe pas de chemin entre le noeud
![]() et un noeud
et un noeud
![]() , alors
, alors
![]() . Revenons maintenant à notre problème de tension compatible. Nous
proposons de transformer le graphe
. Revenons maintenant à notre problème de tension compatible. Nous
proposons de transformer le graphe
![]() en un graphe
en un graphe
![]() où chaque arc
où chaque arc
![]() est dédoublé en deux arcs
est dédoublé en deux arcs
![]() et
et
![]() ,
,
![]() porte la distance
porte la distance
![]() et
et
![]() porte la distance
porte la distance
![]() (cf. figure 3.1). Notons
(cf. figure 3.1). Notons
![]() l'ensemble des arcs
l'ensemble des arcs
![]() et
et
![]() l'ensemble des arcs
l'ensemble des arcs
![]() . Un noeud source
. Un noeud source
![]() est également ajouté, il est connecté à tous les autres
noeuds par un chemin (pour satisfaire à la première partie des conditions
d'optimalité). Pour cela il faut ajouter un ensemble
est également ajouté, il est connecté à tous les autres
noeuds par un chemin (pour satisfaire à la première partie des conditions
d'optimalité). Pour cela il faut ajouter un ensemble
![]() d'arcs de longueur infinie qui relient
d'arcs de longueur infinie qui relient
![]() à tous les noeuds de degré entrant nul.
à tous les noeuds de degré entrant nul.
Si on cherche maintenant la plus courte distance entre le noeud
![]() et tous les autres noeuds, on obtient le vecteur
et tous les autres noeuds, on obtient le vecteur
![]() des plus courtes distances qui satisfait les conditions d'optimalité 3.7 qui peuvent aussi
s'écrire:
des plus courtes distances qui satisfait les conditions d'optimalité 3.7 qui peuvent aussi
s'écrire:
Autrement dit,
![]() . Si on pose la tension
. Si on pose la tension
![]() associée au potentiel
associée au potentiel
![]() , on a alors
, on a alors
![]() ,
,
![]() est donc une tension compatible.
est donc une tension compatible.
Algorithme 3.7: tensionCompatibleCheminBis(graphe
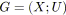 ,tension
,tension
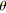 )
)
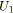

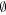 ;
;
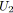

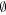 ;
;
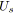

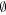 ;
;
pour tout
 faire
faire
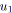

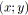 ;
;
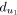

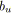 ;
;
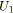

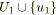 ;
;
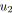

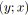 ;
;
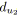

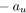 ;
;
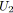

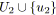 ;
;
fin pour;
pour tout
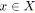 tel que
tel que
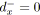 faire
faire
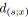

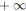 ;
;
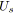

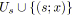 ;
;
fin pour;
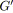

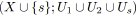 ;
;
plusCourtChemins( ,
,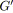 ,
, ,
, );
);
/* Au retour
 associe à chaque noeud sa plus courte distance à
associe à chaque noeud sa plus courte distance à
 . */
. */
pour tout
 faire
faire
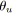

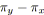 ;
;
fin algorithme; Pour résoudre ce problème des plus courtes distances, nous proposons l'algorithme
3.7 qui utilise la même méthode de résolution de plus court chemin que
l'algorithme 3.1, c'est-à-dire la méthode de label-correcting de Bellman et
Ford que l'on retrouve dans [Ahuja93] et qui est également
disponible dans l'annexe. De la même manière, la détection d'un circuit de
longueur négative dans
![]() signifie qu'il n'y a pas de tension compatible dans
signifie qu'il n'y a pas de tension compatible dans
![]() (grâce à la proposition 3.4 et au fait que les arcs de
(grâce à la proposition 3.4 et au fait que les arcs de
![]() rajoutés n'induisent pas de nouveau circuit). L'algorithme de Bellman et Ford
s'exécute en
rajoutés n'induisent pas de nouveau circuit). L'algorithme de Bellman et Ford
s'exécute en
![]() opérations donc notre algorithme s'exécute également en
opérations donc notre algorithme s'exécute également en
![]() opérations.
opérations.
| CONCLUSION |
En résumé, le tableau 3.1 récapitule les différents algorithmes pour trouver une tension compatible avec leur complexité dans le cas de bornes de tension réelles ou entières.
|
||||||||||||||||||||||
| Tableau 3.1: Complexité des algorithmes de tension compatible. | ||||||||||||||||||||||
Les algorithmes sont classés en fonction de leur efficacité théorique, de la moins bonne à la meilleure. Nous proposons également une campagne de tests numériques afin d'évaluer l'efficacité pratique des différentes méthodes. Pour connaître en détail comment ont été dirigés ces essais (méthode de génération des problèmes, compilateur utilisé...), le lecteur peut consulter l'annexe. Nous précisons seulement ici que les problèmes générés ont des bornes de tension entières. Pour les méthodes de cocycle augmentant, le nombre d'itérations est le nombre de recherches de cocycle effectuées. Les temps de calcul sont exprimés en secondes sur une machine RISC-6000 à 160 MHz.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Tableau 3.2: Résultats numériques pour les algorithmes de tension
compatible, influence de la dimension du graphe. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Le tableau 3.2 montre le temps de calcul de chaque méthode pour différentes
tailles de graphe (avec
![]() ). On s'aperçoit que la méthode de cocycle augmentant 3.5 est plus
efficace que la méthode de plus court chemin 3.3, ce qui n'est pas très
étonnant car sa complexité est fonction de
). On s'aperçoit que la méthode de cocycle augmentant 3.5 est plus
efficace que la méthode de plus court chemin 3.3, ce qui n'est pas très
étonnant car sa complexité est fonction de
![]() qui est très faible dans cette première série de tests.
qui est très faible dans cette première série de tests.
|
||||||||||||||||||||||||||||||||||
| Tableau 3.3: Résultats numériques pour les algorithmes de tension
compatible, influence de l'échelle des tensions. |
||||||||||||||||||||||||||||||||||
Il est donc intéressant de voir le comportement des méthodes en fonction de la
valeur de
![]() . Le tableau 3.3 montre le temps de calcul de chaque méthode pour
différentes valeurs de la borne maximale de tension
. Le tableau 3.3 montre le temps de calcul de chaque méthode pour
différentes valeurs de la borne maximale de tension
![]() sur les arcs (avec
sur les arcs (avec
![]() et
et
![]() ). Comme prévu, la méthode de cocycle augmentant 3.5 varie en fonction de
). Comme prévu, la méthode de cocycle augmentant 3.5 varie en fonction de
![]() alors que les autres méthodes sont stables. Le décalage pour
alors que les autres méthodes sont stables. Le décalage pour
![]() est simplement dû au fait que
est simplement dû au fait que
![]() est trop petit et qu'il "facilite" la résolution du problème
(en effet, en valeurs entières, les possibilités de tension compatible sont trop
réduites voire uniques pour certains arcs).
est trop petit et qu'il "facilite" la résolution du problème
(en effet, en valeurs entières, les possibilités de tension compatible sont trop
réduites voire uniques pour certains arcs).
|
||||||||||||||||||||||||
| Tableau 3.4: Classement théorique et pratique des algorithmes de tension compatible. | ||||||||||||||||||||||||
Enfin le tableau 3.4 classe les méthodes de la moins efficace à la plus efficace, d'un point de vue pratique, et rappelle le classement d'un point de vue théorique. Un rapport des vitesses d'exécution est effectué par rapport à l'algorithme le plus rapide. Il est calculé à partir de la dernière ligne du tableau 3.3 qui nous semble la situation la plus extrême (dimension du graphe et échelle de tension importantes). Bien évidemment, ces résultats numériques dépendent énormément de la manière de programmer les méthodes, mais nous nous sommes efforcés d'implémenter au mieux et de la même manière chaque méthode afin de réduire le plus possible ce genre de biais.
|