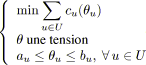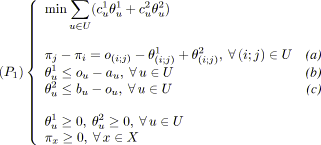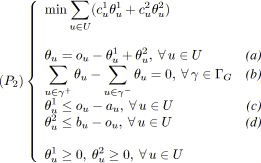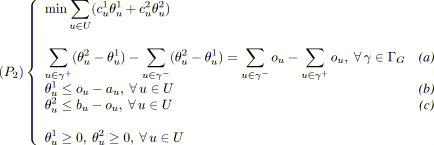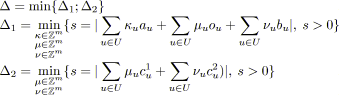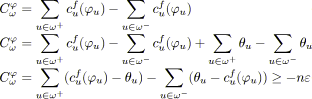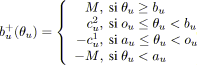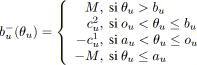|
4. TENSION DE COUT MINIMAL |
Nous nous intéressons ici au problème de la tension de coût minimal.
Il s'agit de trouver une tension
![]() compatible (
compatible (![]() ) dans un graphe
) dans un graphe
![]() , avec
, avec
![]() et
et
![]() . A chaque arc
. A chaque arc
![]() est associée une fonction de coût
est associée une fonction de coût
![]() qui, en fonction de sa tension
qui, en fonction de sa tension
![]() , impute un coût à l'arc
, impute un coût à l'arc
![]() . L'objectif est de minimiser la somme de ces coûts, i.e.
. L'objectif est de minimiser la somme de ces coûts, i.e.
![]() . Dans un premier temps, nous considérons des coûts convexes
linéaires par morceaux (cf. figure 2.11b). Ensuite, nous nous intéressons à
des coûts convexes dérivables (cf. figure 2.11c). Dans ce chapitre nous ne
considérons pas de structure particulière du graphe. Le chapitre suivant sera
consacré à une classe particulière de graphes, les graphes
série-parallèles, beaucoup plus proche des problèmes de synchronisation
hypermédia.
. Dans un premier temps, nous considérons des coûts convexes
linéaires par morceaux (cf. figure 2.11b). Ensuite, nous nous intéressons à
des coûts convexes dérivables (cf. figure 2.11c). Dans ce chapitre nous ne
considérons pas de structure particulière du graphe. Le chapitre suivant sera
consacré à une classe particulière de graphes, les graphes
série-parallèles, beaucoup plus proche des problèmes de synchronisation
hypermédia.
Dans un premier temps, nous montrons comment le problème avec des coûts linéaires par morceaux peut être ramené très simplement à un problème avec des coûts linéaires. Cependant, la taille du graphe résultant devient trop importante pour que l'utilisation d'un algorithme connu sur cette transformation soit efficace en pratique.
Dans le cas de coûts linéaires par morceaux, nous proposons tout d'abord de modéliser le problème sous la forme d'un programme linéaire. Ensuite, nous étudions les conditions d'optimalité du problème et rappelons la notion de conformité (kilter). Deux approches se présentent naturellement pour résoudre le problème. La première consiste à s'inspirer d'un algorithme de flot de coût minimal et à l'adapter à la tension de coût minimal. Pour cela, nous reprenons la méthode proposée dans [Hadjiat96] pour concevoir deux algorithmes de mise à conformité (out-of-kilter), l'un pour des coûts linéaires par morceaux, l'autre pour des coûts dérivables. La seconde approche consiste à transformer le problème de tension de coût minimal en un problème de flot de coût minimal et à résoudre ce dernier avec un algorithme connu très efficace, en l'occurrence un algorithme de mise à l'échelle des coûts (cost-scaling), nous exploitons ici les résultats de l'article [Ahuja99] pour des coûts linéaires par morceaux.
| 4.1 COUTS LINEAIRES PAR MORCEAUX ET COUTS LINEAIRES |
Nous nous intéressons tout d'abord à des coûts linéaires par morceaux, comme
exposé dans le chapitre 2 (cf. 2.11b). La fonction de coût d'un arc
![]() est définie dans un intervalle
est définie dans un intervalle
![]() et est nulle pour la tension
et est nulle pour la tension
![]() , un coût unitaire
, un coût unitaire
![]() est imputé si
est imputé si
![]() et de la même manière, un coût unitaire
et de la même manière, un coût unitaire
![]() est imputé si
est imputé si
![]() . La fonction de coût
. La fonction de coût
![]() d'un arc
d'un arc
![]() s'écrit donc:
s'écrit donc:
Le problème de trouver une tension de coût minimal avec ce genre de fonction de
coût peut être transformé en un problème de tension de coût minimal
avec des coûts linéaires
![]() où
où
![]() et
et
![]() est définie sur un intervalle
est définie sur un intervalle
![]() pour tout arc
pour tout arc
![]() du nouveau problème. La transformation est illustrée par la figure 4.1.
du nouveau problème. La transformation est illustrée par la figure 4.1.
| Figure 4.1: Transformation de coûts linéaires par morceaux en coûts linéaires. |
Elle consiste à transformer le graphe
![]() en un graphe
en un graphe
![]() en représentant simplement chaque arc
en représentant simplement chaque arc
![]() de
de
![]() (avec un coût linéaire par morceaux) par trois arcs
(avec un coût linéaire par morceaux) par trois arcs
![]() ,
,
![]() et
et
![]() de
de
![]() (avec des coûts linéaires) de la manière suivante.
(avec des coûts linéaires) de la manière suivante.
Ainsi, trouver une tension de coût minimal dans le graphe
![]() revient à trouver une tension de coût minimal dans le graphe
revient à trouver une tension de coût minimal dans le graphe
![]() .
.
Preuve:
D'après la figure 4.1, pour tout arc
![]() de
de
![]() , on a, dans le graphe
, on a, dans le graphe
![]() ,
,
![]() . D'après les intervalles de tension définis précédemment
sur
. D'après les intervalles de tension définis précédemment
sur
![]() , il est facile de vérifier que
, il est facile de vérifier que
![]() dans
dans
![]() , qui est le même intervalle que dans
, qui est le même intervalle que dans
![]() .
.
Soit le coût
![]() dans
dans
![]() . Posons
. Posons
![]() et
et
![]() ,
,
![]() . Si la tension est optimale,
. Si la tension est optimale,
![]() et
et
![]() ne peuvent pas être tous les deux non nuls. En effet, supposons que
ne peuvent pas être tous les deux non nuls. En effet, supposons que
![]() ,
,
![]() et
et
![]() , alors
, alors
![]() . Maintenant si on choisit
. Maintenant si on choisit
![]() et
et
![]() , alors
, alors
![]() ne change pas et la tension sur
ne change pas et la tension sur
![]() reste compatible, mais le coût
reste compatible, mais le coût
![]() , ce qui signifie que l'ancienne tension n'était pas optimale. Le même
raisonnement peut être fait dans le cas où
, ce qui signifie que l'ancienne tension n'était pas optimale. Le même
raisonnement peut être fait dans le cas où
![]() . On s'aperçoit alors que le coût
. On s'aperçoit alors que le coût
![]() est défini de la même manière dans
est défini de la même manière dans
![]() et dans
et dans
![]() quand le coût est minimal.
quand le coût est minimal.
![]()
Donc les algorithmes proposés pour des coûts linéaires, dans
[Hadjiat96] par exemple, peuvent être utilisés directement
pour résoudre le problème. Cependant, pour un graphe
![]() à
à
![]() arcs et
arcs et
![]() noeuds, le graphe
noeuds, le graphe
![]() associé a
associé a
![]() arcs et
arcs et
![]() noeuds. En regardant de plus près la complexité des algorithmes connus
pour des coûts linéaires, cette transformation n'est pas exploitable directement en
pratique: les graphes deviennent trop grands et les algorithmes perdent rapidement de leur
efficacité. Nous cherchons donc à adapter ces algorithmes pour qu'ils manipulent
directement des coûts linéaires par morceaux tout en gardant leur efficacité.
noeuds. En regardant de plus près la complexité des algorithmes connus
pour des coûts linéaires, cette transformation n'est pas exploitable directement en
pratique: les graphes deviennent trop grands et les algorithmes perdent rapidement de leur
efficacité. Nous cherchons donc à adapter ces algorithmes pour qu'ils manipulent
directement des coûts linéaires par morceaux tout en gardant leur efficacité.
| 4.2. MODELISATION SOUS FORME DE PROGRAMME LINEAIRE |
En considérant des coûts linéaires par morceaux comme exposé dans le chapitre 2, il est possible de modéliser le problème sous la forme d'un programme linéaire. De manière générale, le problème peut s'écrire sous la forme suivante.
Bien entendu, cette forme n'est a priori pas linéaire. Dans la section
précédente, nous avons vu comment exprimer la fonction objectif sous forme
linéaire, en introduisant pour chaque arc
![]() , deux variables
, deux variables
![]() et
et
![]() telles que:
telles que:
Le coût s'exprime alors:
Il reste donc maintenant à exprimer la tension sous une forme linéaire. Dans le chapitre 2, nous avons vu deux définitions lors de l'introduction aux graphes: l'une basée sur la matrice d'incidence et l'autre sur une base de cycles. Toutes les deux s'expriment sous forme linéaire. Ces approches ont déjà été abordées, la première dans [Buchanan93b] et [Hadjiat96], et la seconde dans [Kim95]. Ce sont d'ailleurs les principales solutions traitées dans la littérature sur la synchronisation hypermédia. Nous exposons ici les deux modèles en proposant une comparaison pratique des deux programmes.
| 4.2.1. Modèle basé sur la matrice d'incidence |
La première définition de la tension s'exprime à l'aide de la matrice
d'incidence
![]() de
de
![]() :
:
![]() ou
ou
![]() . Le problème peut donc être représenté par le programme
suivant.
. Le problème peut donc être représenté par le programme
suivant.
(4.1)
Ce programme contient
![]() variables et
variables et
![]() contraintes.
contraintes.
| 4.2.2. Modèle basé sur une base de cycles |
La seconde définition de la tension s'exprime à l'aide d'une base de cycles
![]() de
de
![]() :
:
![]() ou
ou
![]() . Le problème peut donc être représenté par le programme
suivant.
. Le problème peut donc être représenté par le programme
suivant.
Les variables
![]() peuvent être éliminées en utilisant la contrainte (a) pour
les substituer dans la contrainte (b). Ce qui donne le programme suivant.
peuvent être éliminées en utilisant la contrainte (a) pour
les substituer dans la contrainte (b). Ce qui donne le programme suivant.
(4.2)
Ce programme contient
![]() variables et
variables et
![]() contraintes puisque la base de cycles contient
contraintes puisque la base de cycles contient
![]() cycles.
cycles.
| 4.2.3. Conclusion |
Les deux programmes proposés ici ont quasiment le même nombre de variables et de
contraintes. Il est donc très difficile de déterminer a priori lequel est le plus
efficace. Cependant il faut noter que le second modèle nécessite de déterminer
une base de cycles, algorithme qui s'effectue en
![]() opérations (cf. chapitre 2 et annexe). Nous proposons donc maintenant une
comparaison pratique de la résolution des deux modèles par la méthode du
Simplex (cf. [Werra90]).
opérations (cf. chapitre 2 et annexe). Nous proposons donc maintenant une
comparaison pratique de la résolution des deux modèles par la méthode du
Simplex (cf. [Werra90]).
Pour connaître en détail comment ont été dirigés ces essais (méthode de génération des problèmes, compilateur utilisé...), le lecteur peut consulter l'annexe. Nous précisons seulement que l'outil CPLEX 6.0 a été utilisé avec ses paramètres par défaut pour résoudre les programmes linéaires et que les problèmes générés ont des bornes de tension et des coûts entiers. Le nombre d'itérations est le nombre d'itérations de la méthode du Simplex. Les temps de calcul sont exprimés en secondes sur une machine RISC-6000 à 160 MHz.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Tableau 4.1: Résultats numériques pour les programmes
linéaires de tension de coût minimal, influence de la dimension du graphe. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Le tableau 4.1 montre le temps de génération et de résolution des deux
programmes pour différentes tailles de graphe (avec
![]() ). Pour le programme
). Pour le programme
![]() , ce temps inclut le temps de génération d'une base de cycles. Il est
surprenant de constater que le programme
, ce temps inclut le temps de génération d'une base de cycles. Il est
surprenant de constater que le programme
![]() se résout beaucoup plus rapidement que le programme
se résout beaucoup plus rapidement que le programme
![]() , bien que la comparaison des itérations pour les deux programmes n'explique pas
cet écart. On ne peut pas non plus l'expliquer par le fait que la génération
de
, bien que la comparaison des itérations pour les deux programmes n'explique pas
cet écart. On ne peut pas non plus l'expliquer par le fait que la génération
de
![]() nécessite la construction d'une base de cycles, cette dernière
s'effectuant en un temps négligeable par rapport au temps de résolution (environ
nécessite la construction d'une base de cycles, cette dernière
s'effectuant en un temps négligeable par rapport au temps de résolution (environ
![]() du temps de résolution).
du temps de résolution).
La programmation linéaire est la principale solution implémentée dans les
systèmes de synchronisation hypermédia. Il nous paraît donc intéressant
de comparer les méthodes que nous proposons avec la résolution du programme
linéaire équivalent, en occurrence le modèle
![]() qui est le plus performant.
qui est le plus performant.
| 4.3. CONFORMITE ET OPTIMALITE |
Dans cette section, nous étudions les conditions suffisantes pour qu'une tension ait un coût minimal. Ces conditions sont très similaires aux conditions d'optimalité d'un flot de coût minimal. Elles sont associées à la notion de conformité (kilter). Ces conditions sont connues depuis longtemps pour le flot (cf. [Fulkerson61]). Elles ont ensuite été introduites pour la tension par J.M. Pla (cf. [Pla71]). Nous proposons un rappel de ces conditions et de la notion de conformité tout d'abord pour des coûts linéaires, puis pour des coûts convexes linéaires par morceaux et enfin pour des coûts convexes dérivables.
| 4.3.1. Coûts linéaires |
Nous considérons ici une fonction de coût de la forme
![]() pour chaque arc
pour chaque arc
![]() du graphe. Dans [Pla71], la conformité d'un
arc est définie de la manière suivante.
du graphe. Dans [Pla71], la conformité d'un
arc est définie de la manière suivante.
Soit
|
(4.3) |
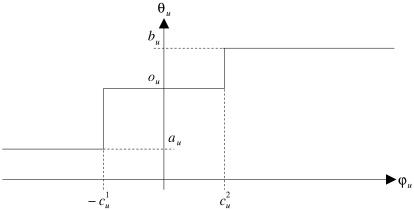
La figure 4.2. illustre cette notion de conformité. La courbe qu'elle représente est appelée courbe de conformité. Quand un arc se trouve sur la courbe, il est conforme. En dehors, il ne l'est plus.
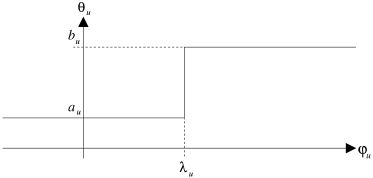 |
| Figure 4.2: Courbe de conformité (coût linéaire). |
J.M. Pla propose le théorème suivant qui associe l'optimalité d'une tension à sa conformité pour chaque arc du graphe.
Soit une tension dans le graphe
. S'il existe un flot
pour lequel tout arc de
est conforme par rapport à
et
, alors
est une tension de coût minimal.
(4.4)
Preuve:
![]() est optimale si et seulement si pour toute tension
est optimale si et seulement si pour toute tension
![]() , on a
, on a
![]() , i.e.
, i.e.
![]() (*). La tension et le flot étant orthogonaux, alors pour tout flot
(*). La tension et le flot étant orthogonaux, alors pour tout flot
![]() on a
on a
![]() . L'inégalité (*) s'écrit alors
. L'inégalité (*) s'écrit alors
![]() ou encore
ou encore
![]() . La conformité par rapport à
. La conformité par rapport à
![]() et
et
![]() de chaque arc induit que les termes de la somme sont tous négatifs (cf.
définition 4.3).
de chaque arc induit que les termes de la somme sont tous négatifs (cf.
définition 4.3).
![]()
| 4.3.2. Coûts linéaires par morceaux |
Nous considérons maintenant pour chaque arc
![]() du graphe une fonction de coût convexe linéaire par morceaux de la forme
suivante (cf. figure 2.11b).
du graphe une fonction de coût convexe linéaire par morceaux de la forme
suivante (cf. figure 2.11b).
En reprenant la transformation de la figure 4.1, un arc
![]() du graphe
du graphe
![]() peut être remplacé par trois arcs
peut être remplacé par trois arcs
![]() ,
,
![]() et
et
![]() dans le graphe
dans le graphe
![]() . Soit
. Soit
![]() une tension dans
une tension dans
![]() et
et
![]() la tension associée dans
la tension associée dans
![]() telle que
telle que
![]() . De la même manière, soit
. De la même manière, soit
![]() un flot dans
un flot dans
![]() et
et
![]() le flot associé dans
le flot associé dans
![]() telle que
telle que
![]() .
.
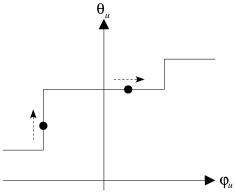
La figure 4.3 montre les courbes de conformité des trois arcs
![]() ,
,
![]() et
et
![]() . La première courbe est volontairement inversée pour faciliter la
compréhension de la construction de la courbe de conformité de
. La première courbe est volontairement inversée pour faciliter la
compréhension de la construction de la courbe de conformité de
![]() (cf. figure 4.4).
(cf. figure 4.4).
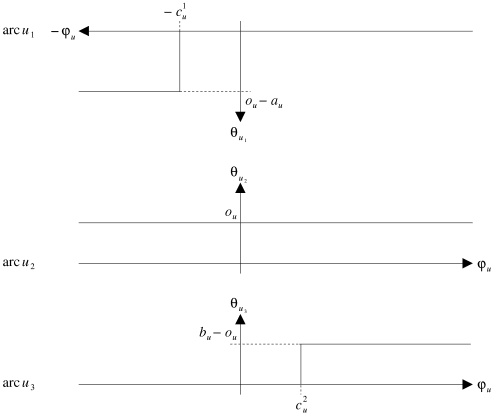 |
| Figure 4.3: Courbe de conformité (transformation en coûts linéaires d'un coût linéaire par morceaux). |
Nous proposons de définir la conformité d'un arc
![]() de la manière suivante. Un arc
de la manière suivante. Un arc
![]() dans le graphe
dans le graphe
![]() est dit conforme par rapport à
est dit conforme par rapport à
![]() et
et
![]() si ses arcs associés dans
si ses arcs associés dans
![]() sont tous les trois conformes par rapport à
sont tous les trois conformes par rapport à
![]() et
et
![]() . Autrement dit,
. Autrement dit,
![]() est conforme si l'une des affirmations suivantes est vérifiée.
est conforme si l'une des affirmations suivantes est vérifiée.
-
 et
et
 ,
,
 ,
,
 , i.e.
, i.e.
 .
.
-
 et
et
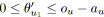 ,
,
 ,
,
 , i.e.
, i.e.
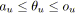 .
.
-
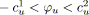 et
et
 ,
,
 ,
,
 , i.e.
, i.e.
 .
.
-
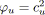 et
et
 ,
,
 ,
,
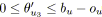 , i.e.
, i.e.
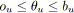 .
.
-
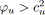 et
et
 ,
,
 ,
,
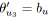 , i.e.
, i.e.
 .
.
En résumé, voici la définition d'un arc conforme.
Soit une tension et
un flot dans le graphe
. Un arc
est dit conforme par rapport à
et
si l'une des affirmations suivantes est vérifiée.
et
.
et
.
et
.
et
.
et
.
(4.5)
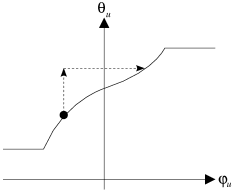
Ce qui se traduit par la courbe de conformité illustrée dans la figure 4.4. Comme
![]() , la courbe se construit simplement en sommant les courbes de conformité des
trois arcs
, la courbe se construit simplement en sommant les courbes de conformité des
trois arcs
![]() ,
,
![]() et
et
![]() (cf. figure 4.3).
(cf. figure 4.3).
 |
| Figure 4.4: Courbe de conformité (coût linéaire par morceaux). |
Comme trouver une tension optimale dans
![]() est équivalent à trouver une tension optimale dans
est équivalent à trouver une tension optimale dans
![]() , une proposition similaire à celle de J.M. Pla peut être établie.
, une proposition similaire à celle de J.M. Pla peut être établie.
Soit une tension dans le graphe
. S'il existe un flot
pour lequel tout arc de
est conforme par rapport à
et
, alors
est une tension de coût minimal.
(4.6)
Nous avons considéré ici une fonction convexe avec deux morceaux linéaires, mais l'étude peut s'appliquer à n'importe quelle fonction convexe linéaire par morceaux. La convexité de la fonction de coût implique que la courbe de conformité sera toujours croissante. La seule différence réside dans le nombre de "paliers" dans la courbe. En fait, il y en a autant que de morceaux linéaires dans la fonction de coût.
| 4.3.3. Coûts dérivables |
Nous considérons ici une fonction de coût convexe dérivable quelconque pour
chaque arc
![]() du graphe. Nous proposons de définir la conformité d'un arc de la
manière suivante.
du graphe. Nous proposons de définir la conformité d'un arc de la
manière suivante.
Soit une tension et
un flot dans le graphe
. Un arc
est dit conforme par rapport à
et
si l'une des affirmations suivantes est vérifiée.
et
.
et
.
et
.
(4.7)
La figure 4.5 est un exemple de courbe de conformité associée à cette définition. Comme la fonction de coût est convexe, cette courbe est toujours croissante.
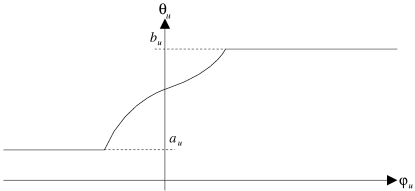 |
| Figure 4.5: Courbe de conformité (coût dérivable). |
Comme pour les coûts linéaires, il est possible d'associer l'optimalité d'une tension à sa conformité pour chaque arc du graphe grâce à la proposition suivante.
Soit une tension dans le graphe
. S'il existe un flot
pour lequel tout arc de
est conforme par rapport à
et
, alors
est une tension de coût minimal.
(4.8)
Preuve:
Soit
![]() une tension et
une tension et
![]() un flot dans
un flot dans
![]() pour lesquels tous les arcs du graphe sont conformes. Quelque soit la tension
pour lesquels tous les arcs du graphe sont conformes. Quelque soit la tension
![]() , il est facile de vérifier que
, il est facile de vérifier que
![]() (*). La fonction
(*). La fonction
![]() étant convexe, on a
étant convexe, on a
![]() (**). (*) et (**) induisent
(**). (*) et (**) induisent
![]() . Donc
. Donc
![]() . La tension et le flot étant orthogonaux,
. La tension et le flot étant orthogonaux,
![]() , d'où
, d'où
![]() , i.e.
, i.e.
![]() , donc
, donc
![]() est de coût minimal.
est de coût minimal.
![]()
| 4.4. METHODE DE MISE A CONFORMITE (COUTS LINEAIRES PAR MORCEAUX) |
D'après la section précédente, quand tous les arcs sont conformes, la tension est optimale. Une idée simple, proposée par J.M. Pla pour des coûts linéaires, consiste à partir d'une tension compatible et d'un flot quelconque, et à amener progressivement tous les arcs sur leur courbe de conformité. Cette méthode, dite de mise à conformité (out-of-kilter) et proposée tout d'abord dans [Fulkerson61] pour le problème du flot de coût minimal, a été adaptée dans [Pla71] pour le problème de la tension de coût minimal dans le cas linéaire. Cette méthode a été également reprise dans [Hadjiat96], toujours pour des coûts linéaires, et propose des variantes usant d'une mise à l'échelle des coûts et des capacités. Nous proposons donc une adaptation relativement immédiate de l'algorithme pour des coûts convexes linéaires par morceaux et reprenons l'étude menée dans [Hadjiat96].
| 4.4.1. Approche directe |
Considérons un arc
![]() qui n'est pas conforme. Le problème ici est de trouver un moyen de rapprocher
cet arc de sa courbe de conformité. Supposons par exemple qu'il soit au dessus. Pour le
rapprocher de sa courbe, il suffit soit d'augmenter son flot, soit de diminuer sa tension. Dans le
chapitre sur la tension compatible (cf. section 3.1.2), nous avons vu que pour modifier la tension
de l'arc
qui n'est pas conforme. Le problème ici est de trouver un moyen de rapprocher
cet arc de sa courbe de conformité. Supposons par exemple qu'il soit au dessus. Pour le
rapprocher de sa courbe, il suffit soit d'augmenter son flot, soit de diminuer sa tension. Dans le
chapitre sur la tension compatible (cf. section 3.1.2), nous avons vu que pour modifier la tension
de l'arc
![]() , il faut trouver un cocycle contenant
, il faut trouver un cocycle contenant
![]() dont tous les arcs acceptent soit l'augmentation, soit la diminution de tension. De la
même manière, si l'on veut modifier le flot de l'arc
dont tous les arcs acceptent soit l'augmentation, soit la diminution de tension. De la
même manière, si l'on veut modifier le flot de l'arc
![]() , il faut trouver un cycle contenant
, il faut trouver un cycle contenant
![]() dont tous les arcs acceptent soit l'augmentation, soit la diminution de flot.
L'idée ici est de trouver une coloration des arcs qui permet d'exploiter le lemme de Minty
pour obtenir de tels cycles et cocycles.
dont tous les arcs acceptent soit l'augmentation, soit la diminution de flot.
L'idée ici est de trouver une coloration des arcs qui permet d'exploiter le lemme de Minty
pour obtenir de tels cycles et cocycles.
| 4.4.1.1. Coloration des arcs |
Voici la coloration proposée dans [Pla71] et [Hadjiat96] pour des coûts linéaires. Nous conservons cette coloration pour des coûts linéaires par morceaux.
- L'arc
 est coloré en vert si une augmentation et une diminution de son flot sont
possibles sans qu'il ne s'éloigne de sa courbe de conformité.
est coloré en vert si une augmentation et une diminution de son flot sont
possibles sans qu'il ne s'éloigne de sa courbe de conformité.
- L'arc
 est coloré en rouge si une augmentation et une diminution de sa tension sont
possibles sans qu'il ne s'éloigne de sa courbe de conformité.
est coloré en rouge si une augmentation et une diminution de sa tension sont
possibles sans qu'il ne s'éloigne de sa courbe de conformité.
- L'arc
 est coloré en noir si une diminution de son flot et une augmentation de sa
tension sont possibles sans qu'il ne s'éloigne de sa courbe de conformité.
est coloré en noir si une diminution de son flot et une augmentation de sa
tension sont possibles sans qu'il ne s'éloigne de sa courbe de conformité.
- L'arc
 est coloré en bleu si une augmentation de son flot et une diminution de sa
tension sont possibles sans qu'il ne s'éloigne de sa courbe de conformité.
est coloré en bleu si une augmentation de son flot et une diminution de sa
tension sont possibles sans qu'il ne s'éloigne de sa courbe de conformité.
La figure 4.6 illustre cette coloration. Les arcs verts et rouges sont forcément conformes. Les arcs verts se trouvent sur les parties horizontales de la courbe (exceptés les angles) et les arcs rouges se trouvent sur les parties verticales de la courbe (exceptés les angles). Les arcs noirs et bleus ne sont pas forcément conformes (seuls les angles de la courbe le sont). Les arcs noirs non conformes sont en dessous de la courbe et les arcs bleus non conformes au dessus. Les arcs bleus et noirs conformes sont les angles de la courbe.
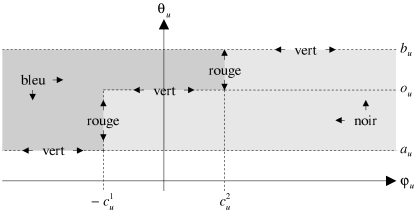 |
| Figure 4.6: Coloration des arcs (coût linéaire par morceaux). |
D'un point de vue pratique, divers cas particuliers comme par exemple
![]() ,
,
![]() ... rendent fastidieuse l'expression algorithmique de la coloration. Cela se complique
encore plus s'il y a plus de deux morceaux dans la fonction de coût. Nous présentons
donc ici la coloration sous forme algorithmique, uniquement dans le cas général.
... rendent fastidieuse l'expression algorithmique de la coloration. Cela se complique
encore plus s'il y a plus de deux morceaux dans la fonction de coût. Nous présentons
donc ici la coloration sous forme algorithmique, uniquement dans le cas général.
- Si
 et
et
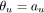 alors
alors
 est vert.
est vert.
- Si
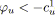 et
et
 alors
alors
 est bleu.
est bleu.
- Si
 et
et
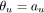 alors
alors
 est noir.
est noir.
- Si
 et
et
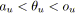 alors
alors
 est rouge.
est rouge.
- Si
 et
et
 alors
alors
 est bleu.
est bleu.
- Si
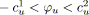 et
et
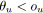 alors
alors
 est noir.
est noir.
- Si
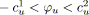 et
et
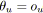 alors
alors
 est vert.
est vert.
- Si
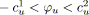 et
et
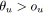 alors
alors
 est bleu.
est bleu.
- Si
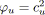 et
et
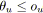 alors
alors
 est noir.
est noir.
- Si
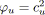 et
et
 alors
alors
 est rouge.
est rouge.
- Si
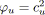 et
et
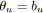 alors
alors
 est bleu.
est bleu.
- Si
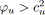 et
et
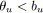 alors
alors
 est noir.
est noir.
- Si
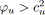 et
et
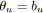 alors
alors
 est vert.
est vert.
| 4.4.1.2. Amélioration de la conformité d'un arc |
A partir de cette coloration que nous noterons
![]() , le lemme de Minty nous permet d'affirmer que pour un arc noir
, le lemme de Minty nous permet d'affirmer que pour un arc noir
![]() non conforme, il existe:
non conforme, il existe:
- soit un cycle contenant
 et des arcs verts, noirs (dans le même sens que
et des arcs verts, noirs (dans le même sens que
 ) ou bleus (dans le sens opposé à
) ou bleus (dans le sens opposé à
 ), ce qui signifie qu'il est possible de diminuer le flot sur ce cycle, autrement dit de
diminuer le flot de
), ce qui signifie qu'il est possible de diminuer le flot sur ce cycle, autrement dit de
diminuer le flot de
 sans éloigner aucun arc de sa courbe de conformité;
sans éloigner aucun arc de sa courbe de conformité;
- soit un cocycle contenant
 et des arcs rouges, noirs (dans le même sens que
et des arcs rouges, noirs (dans le même sens que
 ) ou bleus (dans le sens opposé à
) ou bleus (dans le sens opposé à
 ), ce qui signifie qu'il est possible d'augmenter la tension sur ce cocycle, autrement
dit d'augmenter la tension de
), ce qui signifie qu'il est possible d'augmenter la tension sur ce cocycle, autrement
dit d'augmenter la tension de
 sans éloigner aucun arc de sa courbe de conformité.
sans éloigner aucun arc de sa courbe de conformité.
Cela signifie qu'il est toujours possible de rapprocher un arc noir non conforme de sa courbe de
conformité sans altérer la conformité des autres arcs. Considérons
maintenant la coloration
![]() où tout simplement les couleurs noir et bleu sont inversées par rapport
à la coloration
où tout simplement les couleurs noir et bleu sont inversées par rapport
à la coloration
![]() . Le lemme de Minty permet d'affirmer que pour un arc bleu
. Le lemme de Minty permet d'affirmer que pour un arc bleu
![]() (avec la coloration
(avec la coloration
![]() ) non conforme, il existe:
) non conforme, il existe:
- soit un cycle contenant
 et des arcs verts, noirs (dans le même sens que
et des arcs verts, noirs (dans le même sens que
 ) ou bleus (dans le sens opposé à
) ou bleus (dans le sens opposé à
 ), ce qui signifie qu'il est possible d'augmenter le flot sur ce cycle, autrement dit
d'augmenter le flot de
), ce qui signifie qu'il est possible d'augmenter le flot sur ce cycle, autrement dit
d'augmenter le flot de
 sans éloigner aucun arc de sa courbe de conformité;
sans éloigner aucun arc de sa courbe de conformité;
- soit un cocycle contenant
 et des arcs rouges, noirs (dans le même sens que
et des arcs rouges, noirs (dans le même sens que
 ) ou bleus (dans le sens opposé à
) ou bleus (dans le sens opposé à
 ), ce qui signifie qu'il est possible de diminuer la tension sur ce cocycle, autrement
dit de diminuer la tension de
), ce qui signifie qu'il est possible de diminuer la tension sur ce cocycle, autrement
dit de diminuer la tension de
 sans éloigner aucun arc de sa courbe de conformité.
sans éloigner aucun arc de sa courbe de conformité.
Ce qui signifie qu'il est toujours possible de rapprocher un arc bleu (avec la coloration
![]() ) non conforme de sa courbe de conformité sans altérer la
conformité des autres arcs.
) non conforme de sa courbe de conformité sans altérer la
conformité des autres arcs.
En utilisant les deux colorations (![]() pour un arc en dessous de la courbe,
pour un arc en dessous de la courbe,
![]() pour un arc au dessus de la courbe), il est alors possible de rapprocher n'importe quel
arc non conforme de sa courbe de conformité. Tout ceci permet d'écrire l'algorithme
4.1 proposé en premier lieu dans [Pla71] pour des coûts
linéaires et que nous adaptons ici au cas des coûts linéaires par morceaux.
pour un arc au dessus de la courbe), il est alors possible de rapprocher n'importe quel
arc non conforme de sa courbe de conformité. Tout ceci permet d'écrire l'algorithme
4.1 proposé en premier lieu dans [Pla71] pour des coûts
linéaires et que nous adaptons ici au cas des coûts linéaires par morceaux.
Algorithme 4.1: améliorerConformité(arc,graphe
,
tension,flot
)
siest noir avec
alors
cycleMinty(,
,
,
);
/* Recherche d'un cycle ou d'un cocycle avec. */
sialors
/* Trouver la diminution maximale du flot sur. */

;
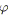

;
sinon
/* Trouver l'augmentation maximale de la tension sur. */


;


;
fin si;
sinon /*est bleu avec
. */
cycleMinty(,
,
,
);
/* Recherche d'un cycle ou d'un cocycle avec. */
sialors
/* Trouver l'augmentation maximale du flot sur. */


;

;
sinon
/* Trouver la diminution maximale de la tension sur. */


;

;
fin si;
fin si;
fin algorithme;
L'algorithme consiste tout d'abord en une recherche d'un cycle ou d'un cocycle basé sur
une coloration, ce qui s'effectue en
![]() opérations. Ensuite, les arcs du cycle (respectivement du cocycle)
trouvé sont parcourus pour déterminer l'augmentation ou la diminution maximale de
flot (respectivement de tension) pouvant être appliquée sur le cycle (respectivement
le cocycle). Tout ceci nécessite
opérations. Ensuite, les arcs du cycle (respectivement du cocycle)
trouvé sont parcourus pour déterminer l'augmentation ou la diminution maximale de
flot (respectivement de tension) pouvant être appliquée sur le cycle (respectivement
le cocycle). Tout ceci nécessite
![]() opérations. L'algorithme complet s'exécute donc en
opérations. L'algorithme complet s'exécute donc en
![]() opérations.
opérations.
| 4.4.1.3. Tension optimale |
L'idée de l'algorithme consiste à sélectionner un arc non conforme et à lui appliquer la procédure d'amélioration pour le rapprocher de sa courbe. Cette opération est répétée jusqu'à ce que tous les arcs soient conformes. Nous commençons tout d'abord par présenter l'algorithme 4.2 dans un contexte général, sans précision du mode de sélection des arcs.
Algorithme 4.2: miseConformitéGénérique(graphe
 ,tension
,tension
 )
)
tensionCompatibleCheminBis( ,
, );
);
/* Recherche d'une tension
compatible. */
 0;
0;
tant que
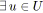 non conforme faire
non conforme faire
sélectionner un tel arc
 non conforme;
non conforme;
améliorerConformité( ,
,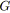 ,
, ,
,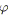 );
);
fin tant que;
fin algorithme;L'algorithme s'exécute en
![]() opérations dans le cas où les bornes de tension et les coûts sont
entiers, et en
opérations dans le cas où les bornes de tension et les coûts sont
entiers, et en
![]() opérations dans le cas où ils sont réels,
opérations dans le cas où ils sont réels,
![]() étant la plus grande borne de tension en valeur absolue, i.e.
étant la plus grande borne de tension en valeur absolue, i.e.
![]() ,
,
![]() étant le plus grand coût en valeur absolue, i.e.
étant le plus grand coût en valeur absolue, i.e.
![]() , et
, et
![]() une borne inférieure de
une borne inférieure de
![]() (cf. algorithme 4.1). Une valeur possible de
(cf. algorithme 4.1). Une valeur possible de
![]() est:
est:
Preuve:
Dans le cas entier, il est évident qu'à chaque amélioration, la tension ou le
flot de l'arc
![]() est amélioré d'au moins 1. Donc, au maximum en
est amélioré d'au moins 1. Donc, au maximum en
![]() itérations,
itérations,
![]() aura atteint sa courbe de conformité. L'algorithme appelle donc
aura atteint sa courbe de conformité. L'algorithme appelle donc
![]() fois la procédure d'amélioration.
fois la procédure d'amélioration.
Dans le cas réel, on s'aperçoit que la tension d'un arc est toujours une combinaison
linéaire (avec des coefficients entiers) des bornes de tension. Autrement dit, pour tout arc
![]() et à toute itération de l'algorithme, il existe
et à toute itération de l'algorithme, il existe
![]() ,
,
![]() et
et
![]() tels que
tels que
![]() . La justification de cette affirmation est similaire à celle
présentée pour l'algorithme 3.5 de tension compatible. De même, le flot d'un
arc est toujours une combinaison linéaire (avec des coefficients entiers) des coûts.
Autrement dit, pour tout arc
. La justification de cette affirmation est similaire à celle
présentée pour l'algorithme 3.5 de tension compatible. De même, le flot d'un
arc est toujours une combinaison linéaire (avec des coefficients entiers) des coûts.
Autrement dit, pour tout arc
![]() et à toute itération de l'algorithme, il existe
et à toute itération de l'algorithme, il existe
![]() et
et
![]() tels que
tels que
![]() . Cela veut dire que la valeur
. Cela veut dire que la valeur
![]() à chaque amélioration est une combinaison linéaire. La plus
petite valeur de
à chaque amélioration est une combinaison linéaire. La plus
petite valeur de
![]() s'exprime donc
s'exprime donc
![]() où
où
![]() et
et
![]() . Les valeurs
. Les valeurs
![]() et
et
![]() existent puisque l'ensemble dans lequel est recherché le minimum est
dénombrable et majoré par 0. A chaque itération, la tension ou le flot de
l'arc
existent puisque l'ensemble dans lequel est recherché le minimum est
dénombrable et majoré par 0. A chaque itération, la tension ou le flot de
l'arc
![]() est améliorée d'au moins
est améliorée d'au moins
![]() . Donc, au maximum en
. Donc, au maximum en
![]() améliorations,
améliorations,
![]() aura atteint sa courbe de conformité. L'algorithme appelle donc
aura atteint sa courbe de conformité. L'algorithme appelle donc
![]() fois la procédure d'amélioration.
fois la procédure d'amélioration.
![]()
Nous nous intéressons maintenant à la méthode de sélection de l'arc à améliorer. Dans [Hadjiat96] et [Pla71], le même arc est sélectionné jusqu'à ce qu'il soit conforme (cf. algorithme 4.3).
Algorithme 4.3: miseConformitéLocale(graphe
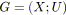 ,tension
,tension
 )
)
tensionCompatibleCheminBis(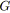 ,
, );
);
 0;
0;
tant que
 non conforme faire
non conforme faire
sélectionner un arc
 non conforme;
non conforme;
tant que
 non conforme faire améliorerConformité(
non conforme faire améliorerConformité( ,
, ,
, ,
, );
);
fin tant que;
fin algorithme;Nous proposons plutôt de considérer les arcs dans un certain ordre et de sélectionner chaque arc non conforme dans cet ordre en n'effectuant qu'une procédure d'amélioration à la fois (cf. algorithme 4.4).
Algorithme 4.4: miseConformitéGlobale(graphe
 ,tension
,tension
 )
)
tensionCompatibleCheminBis( ,
, );
);
 0;
0;
tant que
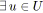 non conforme faire
non conforme faire
pour tout arc
 non conforme faire
non conforme faire
améliorerConformité( ,
,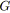 ,
, ,
,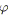 );
);
fin pour;
fin tant que;
fin algorithme;| 4.4.1.4. Conclusion |
Les deux algorithmes proposés ont la même complexité théorique. Il est donc intéressant de les comparer sur le plan pratique. Pour connaître en détail comment ont été dirigés ces essais (méthode de génération des problèmes, compilateur utilisé...), le lecteur peut consulter l'annexe. Nous précisons seulement ici que les problèmes générés ont des bornes de tension et des coûts entiers. Le nombre d'itérations est le nombre de recherches de cycle et de cocycle effectuées. Les temps de calcul sont exprimés en secondes sur une machine RISC-6000 à 160 MHz.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Tableau 4.2: Résultats numériques pour la mise à
conformité (approche directe), influence de la dimension du graphe. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Le tableau 4.2 montre le temps de résolution des deux algorithmes pour
différentes tailles de graphe (avec
![]() ). L'algorithme 4.4, qui n'effectue qu'une amélioration à la fois sur
chaque arc, est le plus performant. La raison intuitive qui nous a fait choisir cette
méthode de sélection des arcs est simplement qu'au lieu de se concentrer sur un arc
et de l'amener sur sa courbe de conformité sans se soucier des autres arcs, il est peut
être plus judicieux d'amener petit à petit tous les arcs sur leur courbe, la
convergence semblant plus globale. On constate également que les deux approches effectuent
à peu près le même nombre de recherches de cycle et de cocycle, mais il
semblerait que dans la seconde approche la recherche soit plus rapide. Notons enfin que ces
résultats sont du même ordre de grandeur que ceux obtenus par la programmation
linéaire (cf. tableau 4.1).
). L'algorithme 4.4, qui n'effectue qu'une amélioration à la fois sur
chaque arc, est le plus performant. La raison intuitive qui nous a fait choisir cette
méthode de sélection des arcs est simplement qu'au lieu de se concentrer sur un arc
et de l'amener sur sa courbe de conformité sans se soucier des autres arcs, il est peut
être plus judicieux d'amener petit à petit tous les arcs sur leur courbe, la
convergence semblant plus globale. On constate également que les deux approches effectuent
à peu près le même nombre de recherches de cycle et de cocycle, mais il
semblerait que dans la seconde approche la recherche soit plus rapide. Notons enfin que ces
résultats sont du même ordre de grandeur que ceux obtenus par la programmation
linéaire (cf. tableau 4.1).
| 4.4.2. Avec une mise à l'échelle |
La méthode de mise à conformité telle qu'elle a été
présentée s'exécute en
![]() opérations pour des bornes de tension et des coûts entiers. Cela signifie
que le temps de calcul est fortement dépendant de l'échelle des coûts et des
bornes de tension, que l'on nomme également capacités. Une méthode dite
mise à l'échelle (scaling) est souvent utilisée pour
réduire cette dépendance avec l'échelle des données.
opérations pour des bornes de tension et des coûts entiers. Cela signifie
que le temps de calcul est fortement dépendant de l'échelle des coûts et des
bornes de tension, que l'on nomme également capacités. Une méthode dite
mise à l'échelle (scaling) est souvent utilisée pour
réduire cette dépendance avec l'échelle des données.
Cette méthode consiste à représenter certaines données sous la forme
d'un polynôme. Pour un entier
![]() , tout entier positif
, tout entier positif
![]() peut s'écrire sous la forme
peut s'écrire sous la forme
![]() où
où
![]() , autrement dit les
, autrement dit les
![]() représentent les chiffres de
représentent les chiffres de
![]() en base
en base
![]() . Pour un ensemble de données
. Pour un ensemble de données
![]() ,
,
![]() doit vérifier:
doit vérifier:
Autrement dit,
![]() ,
,
![]() représentant la partie entière par défaut de
représentant la partie entière par défaut de
![]() .
.
Notons
![]() le problème
le problème
![]() où des données
où des données
![]() sont remplacées par
sont remplacées par
![]() , autrement dit les entiers
, autrement dit les entiers
![]() sont remplacés par leur
sont remplacés par leur
![]() derniers chiffres. La méthode de mise à l'échelle consiste
à résoudre le problème
derniers chiffres. La méthode de mise à l'échelle consiste
à résoudre le problème
![]() en partant de la solution de
en partant de la solution de
![]() . Voici la structure générale de la méthode de mise à
l'échelle.
. Voici la structure générale de la méthode de mise à
l'échelle.
Algorithme 4.5: miseEchelle()


 ;
;
établir une solution
 réalisable pour le problème
réalisable pour le problème
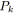 ;
;
tant que
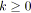 faire
faire
trouver une solution optimale
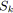 pour le problème
pour le problème
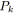
en partant de la solution
 ;
;


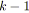 ;
;
adapter la solution
 pour qu'elle soit solution de
pour qu'elle soit solution de
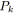 ;
;
fin tant que;
fin algorithme; Pour que la méthode de mise à l'échelle est un intérêt, il
faut que l'algorithme pour résoudre le problème
![]() à partir d'une solution
à partir d'une solution
![]() soit très efficace. Souvent on choisit
soit très efficace. Souvent on choisit
![]() . Dans ce cas, en passant d'une itération à une autre,
. Dans ce cas, en passant d'une itération à une autre,
![]() , ce qui confère généralement des propriétés qui
améliore l'efficacité de l'algorithme (*).
, ce qui confère généralement des propriétés qui
améliore l'efficacité de l'algorithme (*).
| 4.4.2.1. Mise à l'échelle des coûts |
Nous reprenons ici un algorithme présenté dans [Hadjiat96] (pour le cas linéaire) qui effectue une mise à
l'échelle des coûts. L'adaptation à des coûts linéaires par
morceaux est immédiate. Voici donc l'algorithme de mise à l'échelle qui
effectue à chaque itération une mise à conformité de tous les arcs, en
considérant à l'itération
![]() les coûts
les coûts
![]() et
et
![]() pour chaque arc
pour chaque arc
![]() du graphe au lieu des coûts
du graphe au lieu des coûts
![]() et
et
![]() .
.
Algorithme 4.6: miseEchelleCoût(graphe
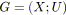 ,tension
,tension
 )
)
tensionCompatibleCheminBis(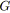 ,
, );
);
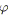
 0;
0;


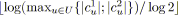 ;
;
tant que
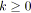 faire
faire
pour tout
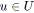 faire
faire
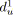

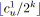 ;
;
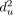

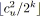 ;
;
pour tout
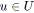 faire
faire
tant que
 non conforme faire
non conforme faire
améliorerConformité( ,
,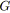 ,
, ,
,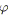 ); /* Avec
); /* Avec
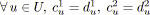 . */
. */
fin tant que;
fin pour;
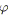

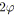 ;
;


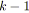 ;
;
fin tant que;
fin algorithme; Dans cet algorithme, la mise à conformité d'un arc s'effectue en
![]() opérations.
opérations.
Preuve:
D'après la remarque (*) énoncée dans l'introduction de cette section,
il est facile de vérifier qu'à chaque itération
![]() , tous les arcs se trouvent à une unité de leur conformité sur la
composante flot. En d'autres termes, les arcs se trouvent à une unité de flot de la
partie verticale de leur courbe de conformité. Dans [Hadjiat96],
il est prouvé que si l'on répète la procédure d'amélioration sur
un arc, le nombre de fois consécutives où l'on améliore la conformité
sur la composante tension, i.e. le nombre de cocycles trouvés, est fini et est borné
par
, tous les arcs se trouvent à une unité de leur conformité sur la
composante flot. En d'autres termes, les arcs se trouvent à une unité de flot de la
partie verticale de leur courbe de conformité. Dans [Hadjiat96],
il est prouvé que si l'on répète la procédure d'amélioration sur
un arc, le nombre de fois consécutives où l'on améliore la conformité
sur la composante tension, i.e. le nombre de cocycles trouvés, est fini et est borné
par
![]() . Autrement dit, avant de trouver un cycle pour modifier le flot (ce qui rendra l'arc
conforme puisqu'il se trouve à une unité de flot de sa courbe de conformité),
il faudra au pire
. Autrement dit, avant de trouver un cycle pour modifier le flot (ce qui rendra l'arc
conforme puisqu'il se trouve à une unité de flot de sa courbe de conformité),
il faudra au pire
![]() améliorations. La procédure d'amélioration s'effectuant en
améliorations. La procédure d'amélioration s'effectuant en
![]() opérations, la mise à conformité d'un arc s'effectue en
opérations, la mise à conformité d'un arc s'effectue en
![]() opérations.
opérations.
![]()
A chaque itération,
![]() opérations sont donc effectuées. L'algorithme de mise à
l'échelle des coûts s'exécute alors en
opérations sont donc effectuées. L'algorithme de mise à
l'échelle des coûts s'exécute alors en
![]() opérations.
opérations.
| 4.4.2.2. Mise à l'échelle des capacités |
Nous reprenons ici un algorithme présenté dans [Hadjiat96] (pour des coûts linéaires) qui effectue une mise
à l'échelle des capacités (i.e. les bornes de tension). L'adaptation à
des coûts linéaires par morceaux est immédiate. Voici donc l'algorithme de mise
à l'échelle qui effectue à chaque itération une mise à
conformité de tous les arcs, en considérant à l'itération
![]() les bornes de tension
les bornes de tension
![]() ,
,
![]() et
et
![]() pour chaque arc
pour chaque arc
![]() au lieu des bornes
au lieu des bornes
![]() ,
,
![]() et
et
![]() (
(![]() représente la partie entière par excès de
représente la partie entière par excès de
![]() ).
).
Algorithme 4.7: miseEchelleCapacité(graphe
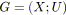 ,tension
,tension
 )
)


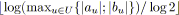 ;
;
pour tout
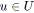 faire
faire
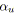

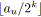 ;
;
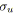

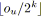 ;
;
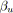

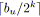 ;
;
tensionCompatibleCheminBis(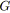 ,
, );
);
/* Avec
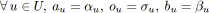 . */
. */
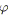
 0;
0;
tant que
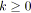 faire
faire
pour tout
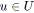 faire
faire
tant que
 non conforme faire
non conforme faire
améliorerConformité( ,
,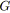 ,
, ,
,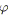 );
);
/* Avec
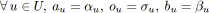 . */
. */
fin tant que;
fin pour;


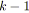 ;
;
pour tout
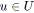 faire
faire
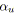

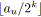 ;
;
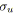

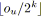 ;
;
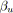

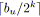 ;
;


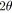 ;
;
fin tant que;
fin algorithme; Dans cet algorithme, la mise à conformité d'un arc s'effectue en
![]() opérations.
opérations.
Preuve:
D'après la remarque (*) énoncée dans l'introduction de cette section,
à chaque itération
![]() , tous les arcs se trouvent à une unité de tension de la partie
horizontale de leur courbe de conformité. Dans [Edmonds72], il
est prouvé que si l'on répète la procédure d'amélioration sur un
arc, le nombre de fois consécutives où l'on améliore la conformité sur
la composante flot, i.e. le nombre de cycles trouvés, est fini et est borné par
, tous les arcs se trouvent à une unité de tension de la partie
horizontale de leur courbe de conformité. Dans [Edmonds72], il
est prouvé que si l'on répète la procédure d'amélioration sur un
arc, le nombre de fois consécutives où l'on améliore la conformité sur
la composante flot, i.e. le nombre de cycles trouvés, est fini et est borné par
![]() . Autrement dit, avant de trouver un cocycle pour modifier la tension (ce qui rendra
l'arc conforme puisqu'il se trouve à une unité de tension de sa courbe de
conformité), il faudra au pire
. Autrement dit, avant de trouver un cocycle pour modifier la tension (ce qui rendra
l'arc conforme puisqu'il se trouve à une unité de tension de sa courbe de
conformité), il faudra au pire
![]() améliorations. La procédure d'amélioration s'effectuant en
améliorations. La procédure d'amélioration s'effectuant en
![]() opérations, la mise à conformité d'un arc s'effectue en
opérations, la mise à conformité d'un arc s'effectue en
![]() opérations.
opérations.
![]()
A chaque itération,
![]() opérations sont donc effectuées. L'algorithme de mise à
l'échelle des capacités s'exécute alors en
opérations sont donc effectuées. L'algorithme de mise à
l'échelle des capacités s'exécute alors en
![]() opérations.
opérations.
Il faut noter que d'une itération
![]() à l'itération
à l'itération
![]() , la tension de certains arcs peut devenir incompatible (seulement d'une unité
de tension). Il faut donc prévoir ce cas dans la coloration des arcs. Par exemple, dans la
coloration
, la tension de certains arcs peut devenir incompatible (seulement d'une unité
de tension). Il faut donc prévoir ce cas dans la coloration des arcs. Par exemple, dans la
coloration
![]() , pour un arc
, pour un arc
![]() , si
, si
![]() alors
alors
![]() est noir et si
est noir et si
![]() alors
alors
![]() est bleu. Ainsi, la procédure d'amélioration aura tendance à
rendre ces arcs compatibles. Si la tension d'un arc
est bleu. Ainsi, la procédure d'amélioration aura tendance à
rendre ces arcs compatibles. Si la tension d'un arc
![]() à une itération
à une itération
![]() ne peut pas être rendue compatible, alors il n'existe plus de cocycle pour
diminuer ou augmenter la tension d'un arc
ne peut pas être rendue compatible, alors il n'existe plus de cocycle pour
diminuer ou augmenter la tension d'un arc
![]() pour le rendre compatible. Le nombre de cycles trouvés consécutivement
étant fini, la procédure finira par trouver un cycle dont le pas
d'amélioration est infini.
pour le rendre compatible. Le nombre de cycles trouvés consécutivement
étant fini, la procédure finira par trouver un cycle dont le pas
d'amélioration est infini.
| 4.4.3. Conclusion |
En résumé, le tableau 4.3 récapitule les trois algorithmes utilisant la mise à conformité pour trouver une tension de coût minimal, avec leur complexité dans le cas de bornes de tension et de coûts réels ou entiers. Les algorithmes sont classés en fonction de leur efficacité théorique, de la moins bonne à la meilleure.
|
||||||||||||||
| Tableau 4.3: Complexité des algorithmes de mise à
conformité pour la tension de coût minimal (coûts linéaires par morceaux). |
||||||||||||||
D'un point de vue théorique, les deux algorithmes de mise à l'échelle sont plus efficaces que l'approche directe de mise à conformité. Cependant, nous proposons ici une comparaison sur le plan pratique de ces trois méthodes. Pour connaître en détail comment ont été dirigés ces essais (méthode de génération des problèmes, compilateur utilisé...), le lecteur peut consulter l'annexe. Nous précisons seulement ici que les problèmes générés ont des bornes de tension et des coûts entiers. Le nombre d'itérations est le nombre de recherches de cycle et de cocycle effectuées. Les temps de calcul sont exprimés en secondes sur une machine RISC-6000 à 160 MHz.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Tableau 4.4: Résultats numériques des algorithmes de mise à
conformité pour la tension de coût minimal (coûts linéaires par morceaux), influence de l'échelle des données. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Le tableau 4.4 montre le temps de résolution des algorithmes pour différentes
valeurs de la borne maximale de tension
![]() et de la borne maximale des coûts
et de la borne maximale des coûts
![]() (avec
(avec
![]() et
et
![]() ) sur un arc. On s'aperçoit tout d'abord que l'approche directe n'est pas
sensible du tout à l'échelle des coûts, ce qui explique que l'algorithme de
mise à l'échelle des coûts soit si peu efficace. En outre, cette mise à
l'échelle rend naturellement la méthode sensible à
) sur un arc. On s'aperçoit tout d'abord que l'approche directe n'est pas
sensible du tout à l'échelle des coûts, ce qui explique que l'algorithme de
mise à l'échelle des coûts soit si peu efficace. En outre, cette mise à
l'échelle rend naturellement la méthode sensible à
![]() . En revanche, l'approche directe est assez sensible à l'échelle des
capacités. La mise à l'échelle des capacités, bien que moins
performante pour les échelles testées que l'approche directe, est très stable,
ce qui laisse présager un très bon comportement, probablement une meilleure
efficacité que l'approche directe, pour des échelles beaucoup plus grandes qu'il nous
est assez difficile de tester pour des raisons de précision dans la représentation
des entiers en machine.
. En revanche, l'approche directe est assez sensible à l'échelle des
capacités. La mise à l'échelle des capacités, bien que moins
performante pour les échelles testées que l'approche directe, est très stable,
ce qui laisse présager un très bon comportement, probablement une meilleure
efficacité que l'approche directe, pour des échelles beaucoup plus grandes qu'il nous
est assez difficile de tester pour des raisons de précision dans la représentation
des entiers en machine.
| 4.5. METHODE DE MISE A CONFORMITE (COUTS DERIVABLES) |
La section 4.3 a montré que pour tous les types de coûts convexes que nous avons choisis d'étudier, si tous les arcs sont conformes alors la tension est optimale. Ainsi, l'idée de la méthode précédente reste valide pour des coûts dérivables: amener progressivement tous les arcs sur leur courbe de conformité. La différence avec les coûts linéaires par morceaux réside dans la définition de la courbe de conformité des arcs.
En effet, dans le cas de coûts linéaires par morceaux, la courbe est formée uniquement de segments verticaux et horizontaux, ce qui signifie qu'un arc qui se trouve sur sa courbe de conformité peut être déplacé sans être écarté de sa courbe, en modifiant soit sa composante flot, soit sa composante tension (cf. figure 4.7). Pour un coût dérivable, la partie principale de la courbe est continue, autrement dit un arc qui se trouve sur la partie croissante de sa courbe de conformité ne peut être déplacé sans être écarté de sa courbe qu'à condition de modifier à la fois sa composante flot et sa composante tension (cf. figure 4.8).
|
|
Il est très difficile d'effectuer un tel déplacement tout en conservant à la fois les propriétés de flot et de tension et tout en n'éloignant aucun arc de sa courbe de conformité. Nous choisissons donc de garder l'approche de la méthode de mise à conformité présentée précédemment et qui consiste à modifier soit le flot d'un cycle, soit la tension d'un cocycle séparément.
Nous proposons alors d'approcher la courbe de conformité pour des coûts
dérivables par une courbe en escalier, avec une précision plus ou moins importante,
ce qui nous garantit un bon fonctionnement de l'algorithme de mise à conformité.
Cette méthode est fortement inspirée d'un algorithme proposé dans
[Berge62] pour résoudre un problème de transport avec des
coûts convexes dérivables. Pour formaliser cette approximation, nous introduisons la
notion d'![]() -conformité, à partir de laquelle nous proposons et
discutons de différentes adaptations de la méthode de mise à conformité
aux coûts dérivables.
-conformité, à partir de laquelle nous proposons et
discutons de différentes adaptations de la méthode de mise à conformité
aux coûts dérivables.
| 4.5.1. Dérivée approchée |
Lorsque la forme algébrique d'une fonction n'est pas connue, le calcul en pratique de sa
dérivée est généralement approché. Afin de préciser cette
approximation, nous introduisons ici la notion d'![]() -dérivée, ou dérivée approchée.
-dérivée, ou dérivée approchée.
On appelle -dérivée d'une fonction
la fonction notée
telle que, pour une précision
donnée:
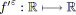
où
, tel que
(4.9)
Dans le cas d'une fonction convexe, on a
![]() , ce qui entraîne
, ce qui entraîne
![]() pour tout
pour tout
![]() (cf. figure 4.9).
(cf. figure 4.9).
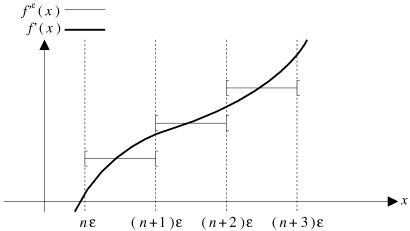 |
| Figure 4.9: Dérivée approchée d'une fonction convexe. |
| 4.5.2. Conformité approchée |
La définition de la conformité d'un arc ayant un coût dérivable a été introduite à la section 4.3. Mais nous avons vu que celle-ci, à cause de sa continuité, empêche le bon fonctionnement de la méthode de mise à conformité. Il nous faudrait une fonction en escalier.
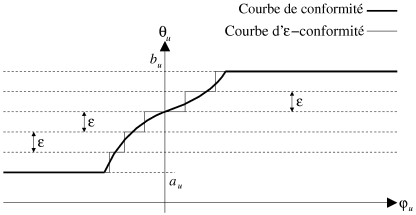 |
| Figure 4.10: Courbe de conformité approchée (mise à conformité). |
Nous introduisons donc la notion d'![]() -conformité, ou conformité
approchée, qui définit la conformité d'un arc non pas par rapport à
sa fonction de coût exacte, mais par rapport à une approximation définie par
une
-conformité, ou conformité
approchée, qui définit la conformité d'un arc non pas par rapport à
sa fonction de coût exacte, mais par rapport à une approximation définie par
une
![]() -dérivée.
-dérivée.
Soit une tension et
un flot dans le graphe
. Un arc
est dit
-conforme par rapport à
et
si l'une des affirmations suivantes est vérifiée.
et
.
et
.
et
.
(4.10)
La figure 4.10 illustre cette notion de conformité approchée. Nous nous retrouvons dans une configuration équivalente à celle d'un coût linéaire par morceaux, ce qui est tout à fait normal puisque l'approximation effectuée sur la dérivée revient à linéariser la fonction de coût.
| 4.5.3. Coloration des arcs |
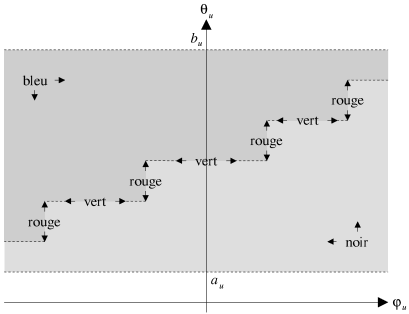 |
| Figure 4.11: Coloration des arcs (coût dérivable). |
Nous pouvons alors utiliser la même coloration que pour les coûts linéaires
par morceaux. Celle-ci est illustrée par la figure 4.11 et se formule de la manière
suivante pour une précision
![]() donnée.
donnée.
Si
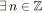 tel que
tel que
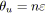 et
et
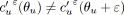 alors
alorssi
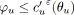 alors
alors
 est bleu;
est bleu;
si
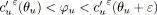 alors
alors
 est vert;
est vert;
si
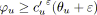 alors
alors
 est noir;
est noir;
sinon
si
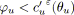 alors
alors
 est bleu;
est bleu;
si
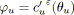 alors
alors
 est rouge;
est rouge;
si
 alors
alors
 est noir.
est noir.
| 4.5.4. Tension optimale |
La première idée pour trouver une tension optimale avec la méthode de mise
à conformité serait de fixer la précision
![]() très petite et de rendre les arcs
très petite et de rendre les arcs
![]() -conformes avec l'algorithme 4.3 ou 4.4. Cependant, en exécutant ces
méthodes on voit très rapidement leur inefficacité face à des courbes
de conformité avec autant de paliers.
-conformes avec l'algorithme 4.3 ou 4.4. Cependant, en exécutant ces
méthodes on voit très rapidement leur inefficacité face à des courbes
de conformité avec autant de paliers.
Intuitivement, au cours des itérations, de plus en plus d'arcs deviennent conformes. Mais un arc conforme est beaucoup plus difficile à déplacer qu'un arc non conforme puisqu'il doit à tout moment rester sur sa courbe de conformité. Autrement dit pour déplacer un arc d'un point de la courbe à un autre, il doit suivre tous les paliers de la courbe qui séparent les deux points, ce qui se traduit par une recherche de cycle ou de cocycle à chaque palier. Il est alors facile de comprendre que pour une précision très petite, le nombre de paliers devient beaucoup trop important pour que la méthode de mise à conformité fonctionne efficacement.
C'est pourquoi nous proposons plutôt une approche qui améliore progressivement
l'approximation de la courbe de conformité (cf. algorithme 4.8). La méthode
présentée démarre avec une valeur très importante pour
![]() . Elle est choisie pour qu'il n'y ait pas plus de dix paliers dans chaque courbe de
conformité. Puis, à chaque itération, tous les arcs sont rendus
. Elle est choisie pour qu'il n'y ait pas plus de dix paliers dans chaque courbe de
conformité. Puis, à chaque itération, tous les arcs sont rendus
![]() -conformes en partant de la solution réalisable obtenue à
l'itération précédente, ensuite la précision est descendue.
L'arrêt s'effectue tout naturellement quand la précision
-conformes en partant de la solution réalisable obtenue à
l'itération précédente, ensuite la précision est descendue.
L'arrêt s'effectue tout naturellement quand la précision
![]() souhaitée est atteinte.
souhaitée est atteinte.
Algorithme 4.8: miseEpsilonConformité(graphe
 ,tension
,tension
 ,réel
,réel
 )
)
tensionCompatibleCheminBis( ,
, );
);


 ;
;
tant que
 faire
faire
rendre tous les arcs
 -conformes;
-conformes;
/* Avec l'algorithme 4.3 ou l'algorithme 4.4. */


 ;
;
fin tant que;
fin algorithme;L'algorithme s'exécute en
![]() opérations. En effet, la méthode de mise à conformité pour des coûts
linéaires par morceaux est appelée
opérations. En effet, la méthode de mise à conformité pour des coûts
linéaires par morceaux est appelée
![]() fois (sa complexité étant
fois (sa complexité étant
![]() ). Il faut noter que la valeur de
). Il faut noter que la valeur de
![]() est différente de celle des coûts linéaires par morceaux. Sa
valeur est plus complexe à exprimer mais représente toujours la plus petite
augmentation possible d'un flot ou d'une tension à une itération donnée (cf.
algorithme 4.2).
est différente de celle des coûts linéaires par morceaux. Sa
valeur est plus complexe à exprimer mais représente toujours la plus petite
augmentation possible d'un flot ou d'une tension à une itération donnée (cf.
algorithme 4.2).
| 4.5.5. Conclusion |
La méthode employée ici appelle un certain nombre de fois la méthode de
mise à conformité, avec chaque fois une précision de plus en plus petite. Il
est intéressant de voir si d'une itération à l'autre la précision a un
impact sur le temps de calcul ou sur le nombre de recherches de cycle et de cocycle. Nous proposons
donc quelques résultats numériques. Pour connaître en détail comment ont
été dirigés ces essais (méthode de génération des
problèmes, compilateur utilisé...), le lecteur peut consulter l'annexe. Nous
précisons seulement ici que les problèmes générés ont des bornes
de tension entières et que la fonction de coût pour chaque arc
![]() est de la forme
est de la forme
![]() avec
avec
![]() choisi aléatoirement entre 0 et 100. Le nombre d'itérations
considéré est le nombre de recherches de cycle et de cocycle effectuées. Les
temps de calcul sont exprimés en secondes sur une machine RISC-6000 à 160 MHz.
choisi aléatoirement entre 0 et 100. Le nombre d'itérations
considéré est le nombre de recherches de cycle et de cocycle effectuées. Les
temps de calcul sont exprimés en secondes sur une machine RISC-6000 à 160 MHz.
Le tableau 4.5 montre le temps de résolution de l'algorithme pour différentes
tailles de graphe (avec
![]() et
et
![]() ). On aurait pu s'attendre à de meilleurs résultats. En effet, pour une
précision de
). On aurait pu s'attendre à de meilleurs résultats. En effet, pour une
précision de
![]() , la méthode de mise à conformité est appelée 6 fois donc
on pourrait supposer un temps 6 fois plus élevé que la méthode pour des
coûts linéaires par morceaux alors que l'on se retrouve avec un rapport de 15. Le
tableau 4.6 apporte des éléments de réponse, il montre l'impact de la
précision sur le temps de résolution et le nombre d'itérations. On
s'aperçoit que le nombre d'itérations reste à peu près le même
pour chaque appel de la méthode de mise à conformité. Par contre, le temps de
calcul augmente quand on commence à avoir une bonne précision et diverge pour une
précision de 100000. Il semblerait donc qu'il soit de plus en plus difficile à mesure
que la précision diminue de rechercher un cycle ou un cocycle. La divergence peut
s'expliquer par le fait que la précision que l'on contrôle se rapproche de la
précision de la machine et qu'il devient très difficile d'exécuter la
méthode.
, la méthode de mise à conformité est appelée 6 fois donc
on pourrait supposer un temps 6 fois plus élevé que la méthode pour des
coûts linéaires par morceaux alors que l'on se retrouve avec un rapport de 15. Le
tableau 4.6 apporte des éléments de réponse, il montre l'impact de la
précision sur le temps de résolution et le nombre d'itérations. On
s'aperçoit que le nombre d'itérations reste à peu près le même
pour chaque appel de la méthode de mise à conformité. Par contre, le temps de
calcul augmente quand on commence à avoir une bonne précision et diverge pour une
précision de 100000. Il semblerait donc qu'il soit de plus en plus difficile à mesure
que la précision diminue de rechercher un cycle ou un cocycle. La divergence peut
s'expliquer par le fait que la précision que l'on contrôle se rapproche de la
précision de la machine et qu'il devient très difficile d'exécuter la
méthode.
|
||||||||||||||||||||||||||||||||
| Tableau 4.5: Résultats numériques de l'algorithme de mise à
pour la tension de coût minimal, influence de la dimension du graphe. |
||||||||||||||||||||||||||||||||
|
||||||||||||||||||||
| Tableau 4.6: Résultats numériques de l'algorithme de mise à
pour la tension de coût minimal, influence de la précision de la courbe. |
||||||||||||||||||||
Cet algorithme est en fait très sensible à la précision de la machine et le fait que l'algorithme puisse fonctionner pour une précision très petite dépend énormément de son implémentation. Il nous a donc semblé important d'éclairer l'éventuel programmeur sur certains problèmes liés à la représentation de l'ensemble des réels par un ensemble dénombrable en machine, ce qui induit forcément des approximations pouvant devenir importantes dans des cas bien précis.
Généralement, un indice sur l'approximation effectuée par l'ordinateur est
donné par une variable
![]() qui est la plus petite valeur supérieure à zéro
représentable par la machine. Ainsi, pour vérifier qu'une variable
qui est la plus petite valeur supérieure à zéro
représentable par la machine. Ainsi, pour vérifier qu'une variable
![]() est égale à une variable
est égale à une variable
![]() , on choisira le test:
, on choisira le test:
![]() et
et
![]() . La relation d'égalité devient alors non transitive: si
. La relation d'égalité devient alors non transitive: si
![]() alors
alors
![]() n'implique pas forcément
n'implique pas forcément
![]() . Cela peut s'avérer problématique pour notre algorithme. Prenons un arc
sur un palier de sa courbe de conformité et cherchons à augmenter son flot sans le
sortir de sa courbe et sans modifier sa tension. L'arc est donc déplacé vers la
droite le long du palier. Une fois arrivé au palier suivant, si la "marche" est
inférieure à
. Cela peut s'avérer problématique pour notre algorithme. Prenons un arc
sur un palier de sa courbe de conformité et cherchons à augmenter son flot sans le
sortir de sa courbe et sans modifier sa tension. L'arc est donc déplacé vers la
droite le long du palier. Une fois arrivé au palier suivant, si la "marche" est
inférieure à
![]() , le déplacement de l'arc peut continuer et ainsi de suite tant que les marches
sont inférieurs à
, le déplacement de l'arc peut continuer et ainsi de suite tant que les marches
sont inférieurs à
![]() . Bien entendu, la tension elle aura changée d'une valeur
considérée différente de zéro, ce qui nuit au bon fonctionnement de
l'algorithme.
. Bien entendu, la tension elle aura changée d'une valeur
considérée différente de zéro, ce qui nuit au bon fonctionnement de
l'algorithme.
Un autre problème classique lié à la représentation des réels
en machine. Si
![]() est une valeur assez grande et
est une valeur assez grande et
![]() une valeur très petite, il y a de grande chance que
une valeur très petite, il y a de grande chance que
![]() . Pour notre algorithme, cela peut se traduire par une boucle infinie. Imaginons qu'un
cycle soit détecté, l'augmentation ou la diminution de flot associée est
effectuée, mais le phénomène précédent se produit, autrement dit
aucune valeur de flot n'est modifiée. A la prochaine itération, on risque de
détecter le même cycle dans les mêmes conditions et ainsi entrer dans une boucle
dont on ne pourra jamais sortir.
. Pour notre algorithme, cela peut se traduire par une boucle infinie. Imaginons qu'un
cycle soit détecté, l'augmentation ou la diminution de flot associée est
effectuée, mais le phénomène précédent se produit, autrement dit
aucune valeur de flot n'est modifiée. A la prochaine itération, on risque de
détecter le même cycle dans les mêmes conditions et ainsi entrer dans une boucle
dont on ne pourra jamais sortir.
| 4.6. METHODE DE MISE A L'ECHELLE DU DUAL |
La méthode proposée ici se limite à des coûts linéaires par morceaux comme définis au chapitre 2 et fournit une tension entière. Pour garantir cette intégrité et le bon fonctionnement de l'algorithme, les bornes de tension et les coûts doivent tous être entiers. Au lieu d'adapter un algorithme de flot à notre problème de tension comme nous l'avons fait avec les méthodes précédentes, nous transformons ici notre problème de tension en un problème de flot. Cette approche a été proposée dans [Ahuja99] pour résoudre un problème intitulé par les auteurs le dual du problème de flot à coûts convexes entiers. Ce problème est une généralisation de notre problème de tension, et par conséquent, l'élaboration de la méthode est plus fastidieuse que celle que nous proposons ici, mais elle aboutit exactement au même résultat.
 |
| Figure 4.12: Etapes de la mise à l'échelle du dual. |
Les grandes étapes de la transformation et de la résolution proposées dans
[Ahuja99] sont illustrées par la figure 4.12. Le problème
de tension de coût minimal est relâché par la technique de la relaxation
Lagrangienne (cf. [Rockafellar84]). Le problème de la recherche
des multiplicateurs de Lagrange est alors simplifié en ajoutant notamment un noeud source
(i.e. sans aucun prédécesseur) dans le graphe. Le problème correspond alors
à un problème de flot de coût minimal que [Ahuja99]
propose de résoudre à l'aide d'une adaptation de l'algorithme de mise à
l'échelle des coûts (cost-scaling) proposé dans [Goldberg87] pour des coûts linéaires et qui opère en
![]() opérations dans sa meilleure implémentation. Les coûts sur les
arcs doivent alors être entiers comme nous l'avons précisé en début de
section. Une fois le flot optimal, la tension obtenue n'est pas forcément entière. La
recherche d'un plus court chemin sur le graphe résiduel est alors effectuée. Cela
peut être fait par l'algorithme de Bellman en
opérations dans sa meilleure implémentation. Les coûts sur les
arcs doivent alors être entiers comme nous l'avons précisé en début de
section. Une fois le flot optimal, la tension obtenue n'est pas forcément entière. La
recherche d'un plus court chemin sur le graphe résiduel est alors effectuée. Cela
peut être fait par l'algorithme de Bellman en
![]() opérations (cf. [Ahuja93]). Les potentiels ainsi
obtenus forment une tension optimale entière pour le problème initial.
opérations (cf. [Ahuja93]). Les potentiels ainsi
obtenus forment une tension optimale entière pour le problème initial.
Le détail de toutes ces étapes pour notre problème spécifique de tension de coût minimal est disponible dans [Boisnard01], mais nous proposons ici une approche plus directe de la transformation du problème de tension de coût minimal en un problème de flot de coût minimal. Il nous a semblé également important de détailler ici l'adaptation de la méthode de mise à l'échelle pour des coûts linéaires par morceaux afin de fournir les éléments nécessaires à l'implémentation de la méthode et de permettre une discussion plus facile sur la méthode par la suite.
| 4.6.1. Transformation en un problème de flot |
Il ne faut pas oublier que la notion de conformité introduite pour les problèmes de tension de coût minimal dans [Pla71] a d'abord été introduite pour les problèmes de flot de coût minimal dans [Fulkerson61] avec les mêmes conditions d'optimalité: lorsque tous les arcs sont conformes, le flot est de coût minimal. En outre, les courbes de conformité sont très semblables. Pour les problèmes de tension, la courbe d'un arc est définie par la dérivée du coût de sa tension, et pour les problèmes de flot, la courbe d'un arc est définie par la dérivée du coût de son flot de la même manière. Ainsi, une courbe de conformité peut être associée au coût d'une tension aussi bien qu'au coût d'un flot. Rechercher une tension de coût minimal dans un graphe revient alors à chercher un flot de coût minimal dans le même graphe, le coût du flot étant déduit de la courbe de conformité décrivant l'optimalité de la tension.
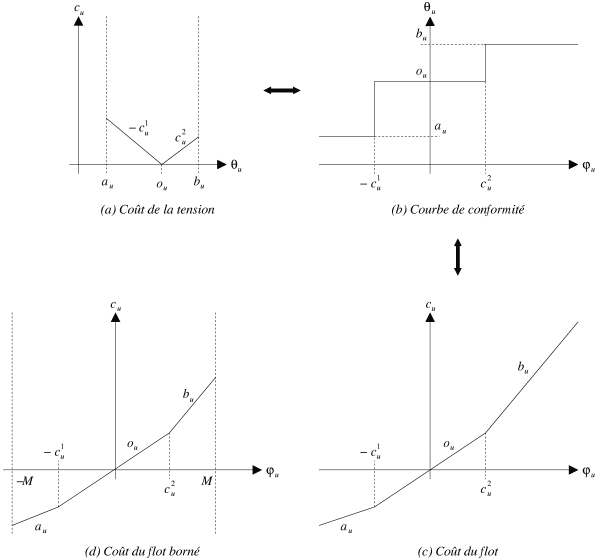 |
| Figure 4.13: Courbe de conformité et fonctions de coûts associées pour le flot et la tension. |
Considérons le problème de tension de coût minimal avec des coûts
linéaires par morceaux. Nous rappelons que la tension
![]() d'un arc
d'un arc
![]() est définie dans l'intervalle
est définie dans l'intervalle
![]() avec un coût comme suit (cf. figure 4.13a).
avec un coût comme suit (cf. figure 4.13a).
A partir de la courbe de conformité traduisant la condition d'optimalité de la tension (cf. figure 4.13b), il est facile d'associer une fonction de coût au flot (cf. figure 4.13c) telle que la courbe de conformité traduise également la condition d'optimalité du flot. Voici l'expression d'une fonction de coût possible.
(4.11)
En observant cette transformation, on s'aperçoit que le flot sur chaque arc n'est pas
borné, ce qui empêche le bon fonctionnement de l'algorithme de mise à
l'échelle des coûts pour le problème de flot. Pour cela, [Ahuja99] propose de remplacer les bornes de la tension de chaque arc par un
coût très élevé
![]() dès que l'on sort de ces bornes (cf. figure 4.14a).
dès que l'on sort de ces bornes (cf. figure 4.14a).
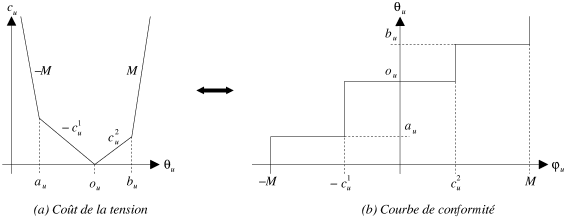 |
| Figure 4.14: Courbe de conformité d'une tension non bornée (coût linéaire par morceaux). |
![]() doit être choisi suffisamment grand pour qu'une tension en dehors des bornes ne
soit jamais optimale. Pour cela il est possible d'affecter une valeur à
doit être choisi suffisamment grand pour qu'une tension en dehors des bornes ne
soit jamais optimale. Pour cela il est possible d'affecter une valeur à
![]() supérieure au coût d'une tension réalisable
supérieure au coût d'une tension réalisable
![]() quelconque. Ainsi, une tension non réalisable aura un coût
forcément supérieur à la tension
quelconque. Ainsi, une tension non réalisable aura un coût
forcément supérieur à la tension
![]() et ne sera donc jamais optimale. La courbe de conformité des arcs pour une
tension minimale est alors légèrement modifiée, mais on s'aperçoit que
le flot associé est compris dans l'intervalle
et ne sera donc jamais optimale. La courbe de conformité des arcs pour une
tension minimale est alors légèrement modifiée, mais on s'aperçoit que
le flot associé est compris dans l'intervalle
![]() (cf. figure 4.14b et figure 4.13d).
(cf. figure 4.14b et figure 4.13d).
Pour résumer, un problème de tension de coût minimal se transforme en un
problème de flot de coût minimal en supprimant les bornes de l'intervalle de tension
(ce qui nécessite le calcul de
![]() et donc la recherche d'une tension réalisable) et en construisant le coût
du flot de chaque arc comme exprimé dans 4.11 et illustré par la figure 4.13d.
et donc la recherche d'une tension réalisable) et en construisant le coût
du flot de chaque arc comme exprimé dans 4.11 et illustré par la figure 4.13d.
Une petite remarque pratique: certaines formulations du problème de flot de coût minimal exigent de n'avoir qu'un seul noeud sans prédécesseur et qu'un seul noeud sans successeur dans le graphe, ce qui est important si l'algorithme utilisé pour résoudre le problème exploite cette particularité. Les deux noeuds sont alors rajoutés en les connectant au graphe par des arcs dont le flot et le coût sont toujours nuls.
| 4.6.2. Flot optimal, mise à l'échelle des coûts |
La méthode de mise à l'échelle des coûts (cost-scaling) pour le problème du flot de coût minimal a été introduite tout d'abord dans [Goldberg87] pour des coûts linéaires. Une analyse détaillée de l'algorithme est également proposée dans [Ahuja93]. L'article [Ahuja99] détaille une adaptation de l'algorithme aux coûts linéaires par morceaux avec son analyse de complexité. La présentation proposée ici de l'algorithme ne fait que résumer les différentes références citées précédemment, le but étant de ne conserver que les détails importants pour notre problème de tension de coût minimal tout en fournissant les éléments essentiels à une éventuelle implémentation. Mais avant toute chose, quelques définitions et propriétés doivent être introduites. Nous invitons également le lecteur à se rapporter à l'ouvrage [Ahuja93] pour toutes les notions de base sur le problème de flot de coût minimal.
| 4.6.2.1. Définitions et propriétés |
Soit
![]() et
et
![]() les valeurs minimales et maximales du flot
les valeurs minimales et maximales du flot
![]() qui traverse l'arc
qui traverse l'arc
![]() . On dit que
. On dit que
![]() est un pseudo-flot si pour tout arc
est un pseudo-flot si pour tout arc
![]() ,
,
![]() , mais ne satisfait pas forcément la conservation des flots à tous les
noeuds.
, mais ne satisfait pas forcément la conservation des flots à tous les
noeuds.
Il a été prouvé (cf. [Fulkerson61]) que si tous
les arcs sont conformes, alors le flot est optimal. Ici est introduite une notion
d'optimalité approchée différente de celle présentée pour
le problème de la tension de coût minimal avec des coûts dérivables. On
dira qu'un flot est ![]() -optimal si tous les arcs du graphe sont à une distance
inférieure ou égale à
-optimal si tous les arcs du graphe sont à une distance
inférieure ou égale à
![]() de leur courbe de conformité sur la composante tension. La figure 4.15 illustre
cette notion, les arcs situés dans les parties grisées ou directement sur la courbe
sont
de leur courbe de conformité sur la composante tension. La figure 4.15 illustre
cette notion, les arcs situés dans les parties grisées ou directement sur la courbe
sont ![]() -conformes.
-conformes.
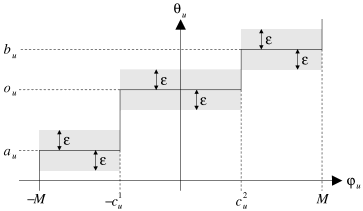 |
| Figure 4.15: Courbe de conformité approchée (mise à l'échelle du dual). |
Notons
![]() la courbe de conformité d'un arc
la courbe de conformité d'un arc
![]() définie seulement sur
définie seulement sur
![]() . Lorsque le flot est
. Lorsque le flot est
![]() -optimal, pour tout arc
-optimal, pour tout arc
![]() dont le flot peut être modifié sans quitter la courbe (i.e.
dont le flot peut être modifié sans quitter la courbe (i.e.
![]() ), on peut affirmer que
), on peut affirmer que
![]() . Ainsi, pour tout cycle augmentant, i.e. dont on peut augmenter le flot, on peut
calculer le coût unitaire d'augmentation
. Ainsi, pour tout cycle augmentant, i.e. dont on peut augmenter le flot, on peut
calculer le coût unitaire d'augmentation
![]() et affirmer:
et affirmer:
Ainsi, si
![]() , alors
, alors
![]() . Comme les coûts sont entiers, cela signifie que
. Comme les coûts sont entiers, cela signifie que
![]() . En outre, il est prouvé que si pour tout cycle
. En outre, il est prouvé que si pour tout cycle
![]() ,
,
![]() , alors
, alors
![]() est optimal (cf. [Ahuja93]). En résumé, un
flot
est optimal (cf. [Ahuja93]). En résumé, un
flot
![]() -optimal est également optimal.
-optimal est également optimal.
| 4.6.2.2. Procédure principale |
L'algorithme de mise à l'échelle des coûts consiste donc à partir
d'une tension
![]() (associée au potentiel
(associée au potentiel
![]() ) nulle et d'un flot
) nulle et d'un flot
![]() compatible (dans notre cas, le flot nul est compatible). On choisit un
compatible (dans notre cas, le flot nul est compatible). On choisit un
![]() de départ suffisamment grand pour que le flot soit
de départ suffisamment grand pour que le flot soit
![]() -optimal. Il est facile de vérifier que prendre
-optimal. Il est facile de vérifier que prendre
![]() suffit. Ensuite, la méthode consiste à diviser
suffit. Ensuite, la méthode consiste à diviser
![]() par deux à chaque itération. Chaque fois, une procédure dite
d'amélioration tente de construire un flot
par deux à chaque itération. Chaque fois, une procédure dite
d'amélioration tente de construire un flot
![]() -optimal à partir du flot
-optimal à partir du flot
![]() -optimal obtenu à l'itération précédente. L'algorithme
s'arrête lorsque
-optimal obtenu à l'itération précédente. L'algorithme
s'arrête lorsque
![]() est inférieur à
est inférieur à
![]() (le flot est alors optimal) et exécute donc
(le flot est alors optimal) et exécute donc
![]() fois la procédure d'amélioration (cf. algorithme 4.9).
fois la procédure d'amélioration (cf. algorithme 4.9).
Algorithme 4.9: flotMinimal(graphe
 ,flot
,flot
 )
)

 0;
0;


 ;
;
trouver un flot
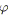 compatible;
compatible;
tant que
 faire
faire
rendreFlotEpsilonOptimal( ,
, ,
,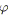 ,
, );
);


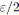 ;
;
fin tant que;
fin algorithme;| 4.6.2.3. Procédure d'amélioration |
La procédure décrite ici consiste à passer d'un flot
![]() -optimal à un flot
-optimal à un flot
![]() -optimal. Tout d'abord, le flot est transformé en un pseudo-flot
-optimal. Tout d'abord, le flot est transformé en un pseudo-flot
![]() -optimal. Pour cela, les arcs sont plaqués sur la courbe en modifiant seulement
la composante flot. Ainsi, si un arc se trouve à gauche de la courbe (i.e. au dessus
à
-optimal. Pour cela, les arcs sont plaqués sur la courbe en modifiant seulement
la composante flot. Ainsi, si un arc se trouve à gauche de la courbe (i.e. au dessus
à
![]() près) alors son flot est augmenté jusqu'à toucher la courbe. A
l'inverse, si un arc se trouve à droite de la courbe (i.e. en dessous à
près) alors son flot est augmenté jusqu'à toucher la courbe. A
l'inverse, si un arc se trouve à droite de la courbe (i.e. en dessous à
![]() près) alors son flot est diminué jusqu'à toucher la courbe (cf.
figure 4.16).
près) alors son flot est diminué jusqu'à toucher la courbe (cf.
figure 4.16).
|
|
La courbe de conformité
![]() n'est pas définie pour
n'est pas définie pour
![]() ,
,
![]() ,
,
![]() et
et
![]() . Il est donc nécessaire de définir une courbe de conformité
à droite
. Il est donc nécessaire de définir une courbe de conformité
à droite
![]() et une courbe de conformité à gauche
et une courbe de conformité à gauche
![]() de la manière suivante, avec
de la manière suivante, avec
![]() .
.
Comme nous le verrons par la suite, il est également nécessaire de pouvoir
déterminer l'augmentation ou la diminution maximale du flot d'un arc sans que ce dernier ne
s'éloigne de sa courbe (soit il est déjà dessus et il n'en sort pas, soit il
n'y est pas encore et alors il s'en rapproche). De cette manière, des modifications du flot
sur le graphe peuvent être effectuées sans altérer la conformité des
arcs. Pour cela, nous définissons une borne à droite notée
![]() et une borne à gauche notée
et une borne à gauche notée
![]() .
.
Voici donc la procédure qui transforme un flot
![]() -optimal en un pseudo-flot
-optimal en un pseudo-flot
![]() -optimal d'après les définitions précédentes.
-optimal d'après les définitions précédentes.
Algorithme 4.10: construirePseudoFlot(graphe,potentiel
,
flot,réel
)
pour tout arcfaire
sialors

;
sinon sialors

;
fin pour;
fin algorithme;
Il est évident que la conservation des flots n'est plus respectée. Il s'agit
maintenant de modifier le pseudo-flot pour qu'il devienne un flot tout en maintenant l'![]() -optimalité. Pour cela, on cherche un noeud
-optimalité. Pour cela, on cherche un noeud
![]() pour lequel il y a un excédent de flot (i.e.
pour lequel il y a un excédent de flot (i.e.
![]() ) et on évacue le surplus de flot à travers les arcs adjacents au noeud.
Cette opération est effectuée jusqu'à ce que tous les noeuds soient
équilibrés, i.e. la conservation des flots est respectée (cf. algorithme
4.11).
) et on évacue le surplus de flot à travers les arcs adjacents au noeud.
Cette opération est effectuée jusqu'à ce que tous les noeuds soient
équilibrés, i.e. la conservation des flots est respectée (cf. algorithme
4.11).
Algorithme 4.11: rendreFlotEpsilonOptimal(graphe,potentiel
,
flot,réel
)
construirePseudoFlot(,
,
,
);
tant queexcédentaire faire
sélectionner un noeudexcédentaire;
équilibrerNoeud(,
,
,
);
fin tant que;
fin algorithme;
Pour équilibrer un noeud, il faut donc trouver des arcs sortants (respectivement
entrants) pour lesquels on peut augmenter (respectivement diminuer) le flot sans quitter la courbe
de conformité (à
![]() près) (cf. algorithme 4.12). Pour éviter tout cyclage de l'algorithme
(cf. [Ahuja93]), on n'augmentera un flot sur un arc que si l'arc se
trouve au dessus de la courbe et à l'inverse on ne diminuera un flot sur un arc que si l'arc
se trouve en dessous de la courbe (cf. figure 4.17). Les arcs remplissant toutes ces conditions
sont dits admissibles.
près) (cf. algorithme 4.12). Pour éviter tout cyclage de l'algorithme
(cf. [Ahuja93]), on n'augmentera un flot sur un arc que si l'arc se
trouve au dessus de la courbe et à l'inverse on ne diminuera un flot sur un arc que si l'arc
se trouve en dessous de la courbe (cf. figure 4.17). Les arcs remplissant toutes ces conditions
sont dits admissibles.
Algorithme 4.12: équilibrerNoeud(noeud
 ,potentiel
,potentiel
 ,flot
,flot
 ,réel
,réel
 )
)


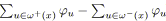 ;
;
tant que
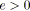 faire
faire
si
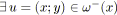 tel que
tel que
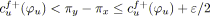
et
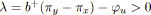 alors
alors
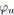

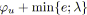 ;
;


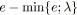 ;
;
sinon si
 tel que
tel que
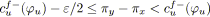
et
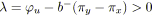 alors
alors
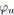

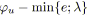 ;
;


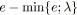 ;
;
sinon
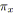

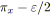 ;
;
fin tant que;
fin algorithme; Si tout le flot n'a pas pu être évacué, on diminue alors le potentiel du
noeud de
![]() , ainsi la tension des arcs sortants augmente (respectivement la tension des arcs
entrants diminue), rapprochant ainsi ces arcs d'une possibilité d'augmentation de leur flot
(cf. figure 4.17) tout en n'éloignant aucun arc de sa courbe de conformité. Ces
opérations d'évacuation de flot et de baisse de potentiel sont
répétées alternativement jusqu'à ce que le noeud soit
équilibré (i.e. la conservation des flots à son niveau est
vérifiée). L'algorithme 4.12 détaille la procédure d'équilibrage
d'un noeud.
, ainsi la tension des arcs sortants augmente (respectivement la tension des arcs
entrants diminue), rapprochant ainsi ces arcs d'une possibilité d'augmentation de leur flot
(cf. figure 4.17) tout en n'éloignant aucun arc de sa courbe de conformité. Ces
opérations d'évacuation de flot et de baisse de potentiel sont
répétées alternativement jusqu'à ce que le noeud soit
équilibré (i.e. la conservation des flots à son niveau est
vérifiée). L'algorithme 4.12 détaille la procédure d'équilibrage
d'un noeud.
Dans [Ahuja99], il est prouvé que la procédure
d'amélioration effectue
![]() diminutions de potentiel,
diminutions de potentiel,
![]() évacuations saturantes et
évacuations saturantes et
![]() évacuations non saturantes, saturante signifiant que l'arc
impliqué dans l'évacuation est saturé, i.e. son flot a atteint sa limite (
évacuations non saturantes, saturante signifiant que l'arc
impliqué dans l'évacuation est saturé, i.e. son flot a atteint sa limite (![]() ou
ou
![]() ). La procédure d'amélioration s'exécute donc en
). La procédure d'amélioration s'exécute donc en
![]() opérations.
opérations.
| 4.6.3. Tension optimale |
Toutes les données du problème sont entières, il est alors facile de
vérifier que le flot obtenu est entier. Cependant, la tension n'est pas entière,
puisque les augmentations ou les diminutions se font avec un pas
![]() rarement entier. Il faut donc maintenant rendre la tension obtenue entière. Pour
cela, il suffit de remplacer pour chaque arc
rarement entier. Il faut donc maintenant rendre la tension obtenue entière. Pour
cela, il suffit de remplacer pour chaque arc
![]() du graphe
du graphe
![]() l'intervalle de tension
l'intervalle de tension
![]() par
par
![]() . Ensuite, on cherche une tension réalisable qui existe forcément puisque
la solution déjà obtenue par la mise à l'échelle du dual est
réalisable. On utilisera par exemple l'algorithme 3.7 (cf. section 3.2) qui garantit une
solution entière. Ainsi, on obtient une tension et un flot parfaitement sur la courbe de
conformité, et tous les deux entiers. En résumé, voici la procédure
pour trouver une tension de coût minimal par l'approche duale.
. Ensuite, on cherche une tension réalisable qui existe forcément puisque
la solution déjà obtenue par la mise à l'échelle du dual est
réalisable. On utilisera par exemple l'algorithme 3.7 (cf. section 3.2) qui garantit une
solution entière. Ainsi, on obtient une tension et un flot parfaitement sur la courbe de
conformité, et tous les deux entiers. En résumé, voici la procédure
pour trouver une tension de coût minimal par l'approche duale.
Algorithme 4.13: miseEchelleDual(graphe
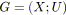 ,tension
,tension
 )
)
tensionCompatibleCheminBis(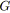 ,
, );
);
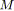

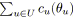 ;
;
construire les coûts du problème de flot équivalent;
/* En utilisant
 . */
. */
flotMinimal(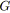 ,
,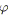 );
);
pour tout arc
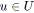
remplacer les bornes de tension
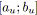 par
par
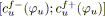 ;
;
tensionCompatibleCheminBis( ,
, );
);
fin algorithme;Nous avons vu au cours de cette présentation que la complexité de l'algorithme de
mise à l'échelle pour le problème de flot s'exécute en
![]() opérations (en utilisant la structure d'arbre dynamique introduite dans
[Sleator83], [Ahuja99] explique que
l'algorithme s'exécute en
opérations (en utilisant la structure d'arbre dynamique introduite dans
[Sleator83], [Ahuja99] explique que
l'algorithme s'exécute en
![]() ). L'étape de transformation du problème de tension en un problème
de flot nécessite la recherche d'une tension compatible (en
). L'étape de transformation du problème de tension en un problème
de flot nécessite la recherche d'une tension compatible (en
![]() opérations avec l'algorithme 3.7), la transformation elle-même est
linéaire (avec
opérations avec l'algorithme 3.7), la transformation elle-même est
linéaire (avec
![]() opérations). Enfin, l'étape de mise en valeur entière de la
tension nécessite également une recherche de tension compatible (en
opérations). Enfin, l'étape de mise en valeur entière de la
tension nécessite également une recherche de tension compatible (en
![]() opérations). La méthode proposée ici, que nous nommerons par la
suite mise à l'échelle du dual, nécessite
opérations). La méthode proposée ici, que nous nommerons par la
suite mise à l'échelle du dual, nécessite
![]() opérations dans sa version générique qui est celle
implémentée pour notre étude.
opérations dans sa version générique qui est celle
implémentée pour notre étude.
| 4.6.4. Conclusion |
D'un point de vue théorique, la méthode de mise à l'échelle du dual,
avec
![]() opérations, est plus efficace que la méthode de mise à
conformité, avec
opérations, est plus efficace que la méthode de mise à
conformité, avec
![]() opérations. Cependant, les complexités sont trop proches pour être
catégorique. Nous proposons donc une comparaison sur le plan pratique des deux
méthodes. Pour connaître en détails comment ont été
dirigés ces essais (méthode de génération des problèmes,
compilateur utilisé...), le lecteur peut consulter l'annexe. Nous précisons seulement
ici que les problèmes générés ont des bornes de tension et des
coûts entiers. Le nombre d'itérations pour la méthode de mise à
conformité est le nombre de recherches de cycle et de cocycle effectuées. Pour la
méthode de mise à l'échelle du dual, le nombre d'itérations est le
nombre d'évacuations de flot effectuées. Les temps de calcul sont exprimés en
secondes sur une machine RISC-6000 à 160 MHz.
opérations. Cependant, les complexités sont trop proches pour être
catégorique. Nous proposons donc une comparaison sur le plan pratique des deux
méthodes. Pour connaître en détails comment ont été
dirigés ces essais (méthode de génération des problèmes,
compilateur utilisé...), le lecteur peut consulter l'annexe. Nous précisons seulement
ici que les problèmes générés ont des bornes de tension et des
coûts entiers. Le nombre d'itérations pour la méthode de mise à
conformité est le nombre de recherches de cycle et de cocycle effectuées. Pour la
méthode de mise à l'échelle du dual, le nombre d'itérations est le
nombre d'évacuations de flot effectuées. Les temps de calcul sont exprimés en
secondes sur une machine RISC-6000 à 160 MHz.
Le tableau 4.7 montre le temps de résolution des algorithmes pour différentes
tailles de graphe (avec
![]() ). On s'aperçoit que la mise à l'échelle du dual est nettement
plus rapide que la mise à conformité, avec en plus un temps de calcul qui croît
beaucoup moins vite.
). On s'aperçoit que la mise à l'échelle du dual est nettement
plus rapide que la mise à conformité, avec en plus un temps de calcul qui croît
beaucoup moins vite.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Tableau 4.7: Résultats numériques de l'algorithme de mise à
l'échelle pour la tension de coût minimal, influence de la dimension du graphe. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Le tableau 4.8 montre le temps de résolution des algorithmes pour différentes
valeurs de la borne maximale de tension
![]() et de la borne maximale des coûts
et de la borne maximale des coûts
![]() (avec
(avec
![]() et
et
![]() ). Comme prévu, la méthode duale est influencée par
l'échelle des capacités puisque ce sont ces dernières qui deviennent les
coûts mis à l'échelle dans le problème de flot. Cette sensibilité
est du même ordre que celle constatée avec l'approche directe de la mise à
conformité. En revanche, l'échelle des coûts (qui devient, par
l'intermédiaire de
). Comme prévu, la méthode duale est influencée par
l'échelle des capacités puisque ce sont ces dernières qui deviennent les
coûts mis à l'échelle dans le problème de flot. Cette sensibilité
est du même ordre que celle constatée avec l'approche directe de la mise à
conformité. En revanche, l'échelle des coûts (qui devient, par
l'intermédiaire de
![]() , l'échelle des capacités dans le problème de flot) n'a aucun
impact sur la méthode duale.
, l'échelle des capacités dans le problème de flot) n'a aucun
impact sur la méthode duale.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Tableau 4.8: Résultats numériques de l'algorithme de mise à
l'échelle pour la tension de coût minimal, influence de l'échelle des données. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Il faut rappeler que la méthode utilisée pour résoudre le problème
de flot n'est pas la plus efficace. Dans [Ahuja93] sont décrits
des algorithmes dont l'efficacité théorique est bien meilleure, cependant ces
algorithmes utilisent tous une mise à l'échelle des capacités (i.e. les
coûts pour le problème de tension) et introduisent donc dans l'expression de leur
complexité un terme fonction de
![]() . Dans l'étude de la méthode de mise à conformité, nous
nous sommes aperçu qu'introduire une sensibilité à
. Dans l'étude de la méthode de mise à conformité, nous
nous sommes aperçu qu'introduire une sensibilité à
![]() n'était pas efficace en pratique. Nous ne savons pas si cela se produirait avec
l'approche duale, mais vus les très bons résultats fournis par la mise à
l'échelle des coûts, nous n'avons pas désiré investir dans le
développement d'une mise à l'échelle des capacités sans être
sûrs du gain de performance.
n'était pas efficace en pratique. Nous ne savons pas si cela se produirait avec
l'approche duale, mais vus les très bons résultats fournis par la mise à
l'échelle des coûts, nous n'avons pas désiré investir dans le
développement d'une mise à l'échelle des capacités sans être
sûrs du gain de performance.
Notre version de la mise à l'échelle ne précise pas l'ordre de parcours des
noeuds pour rendre un flot
![]() -optimal (cf. algorithme 4.11). Une meilleure stratégie,
l'implémentation par vague (wave implementation) proposée dans
[Ahuja93], permet de réduire la complexité de la mise
à l'échelle à
-optimal (cf. algorithme 4.11). Une meilleure stratégie,
l'implémentation par vague (wave implementation) proposée dans
[Ahuja93], permet de réduire la complexité de la mise
à l'échelle à
![]() opérations. Elle propose d'équilibrer les noeuds suivant un ordre
topologique: en considérant le sous-graphe de
opérations. Elle propose d'équilibrer les noeuds suivant un ordre
topologique: en considérant le sous-graphe de
![]() composé uniquement des arcs admissibles, un noeud est classé
après tous ses prédécesseurs. L'existence de cet ordre est garanti (le
sous-graphe est sans circuit), mais est remis en cause à chaque modification de potentiel
(heureusement, l'ordre peut être rétabli en
composé uniquement des arcs admissibles, un noeud est classé
après tous ses prédécesseurs. L'existence de cet ordre est garanti (le
sous-graphe est sans circuit), mais est remis en cause à chaque modification de potentiel
(heureusement, l'ordre peut être rétabli en
![]() opérations). Nous avons implémenté cette stratégie sans
réel succès: le nombre d'itérations et le temps de calcul ne changent pas de
manière significative. Toutes les comparaisons et les discussions futures se feront donc sur
notre version de la méthode.
opérations). Nous avons implémenté cette stratégie sans
réel succès: le nombre d'itérations et le temps de calcul ne changent pas de
manière significative. Toutes les comparaisons et les discussions futures se feront donc sur
notre version de la méthode.
| CONCLUSION |
Nous proposons le tableau 4.9 récapitulant, par ordre d'apparition, les méthodes présentées dans ce chapitre. La complexité de chacune est rappelée pour différentes conditions. Si aucune complexité n'est indiquée, cela signifie que la méthode telle que nous l'avons présentée ne peut pas être appliquée avec les conditions données.
|
||||||||||||||||||||||||||
| Tableau 4.9: Complexité des algorithmes de tension de coût minimal. | ||||||||||||||||||||||||||
Nous proposons également un classement pratique des méthodes pour des coûts linéaires par morceaux et des données entières. Les algorithmes sont classés du moins efficace au plus efficace. Un rapport des vitesses d'exécution est effectué par rapport à l'algorithme le plus rapide. Il est calculé à partir de la dernière ligne des tableaux 4.8 et 4.4 qui nous semble être la situation la plus extrême (dimension du graphe et échelle de tension importantes). Bien évidemment, ce classement est discutable, notamment sur le fait que les résultats numériques dépendent énormément de la manière de programmer les méthodes, mais nous nous sommes efforcés d'implémenter au mieux et de la même manière chaque méthode afin de réduire ce genre de biais. Le classement théorique des méthodes est également rappelé.
|
||||||||||||||||||||||||
| Tableau 4.10: Classement théorique et pratique des algorithmes de tension de coût minimal. | ||||||||||||||||||||||||
Indiscutablement, l'algorithme de mise à l'échelle est le plus efficace. Mais les
tests effectués ici ont porté sur des graphes totalement aléatoires et sur la
recherche d'une tension optimale sans solution de départ spécifique. Nous verrons
dans le chapitre suivant que les graphes utilisés pour la synchronisation hypermédia
ont une structure bien particulière et que l'algorithme de mise à l'échelle a
un comportement moins satisfaisant dans cette situation. Il serait également
intéressant de se pencher sur l'aspect temps réel de la synchronisation
hypermédia et donc d'étudier le comportement des méthodes sur le changement
tout simplement des données d'un arc. Pour la méthode de mise à
conformité, repartir de la tension anciennement optimale pour trouver la nouvelle tension
optimale ne semble pas difficile puisque tous les arcs seraient conformes sauf un, donc en
![]() opérations, l'optimalité est atteinte. Pour la mise à
l'échelle du dual, il est également possible de repartir de la tension optimale. Un
seul arc n'est pas conforme, mais tout le processus de mise à l'échelle doit
être fait et il est possible durant une phase d'amélioration d'altérer la
conformité d'autres arcs à cause d'un
opérations, l'optimalité est atteinte. Pour la mise à
l'échelle du dual, il est également possible de repartir de la tension optimale. Un
seul arc n'est pas conforme, mais tout le processus de mise à l'échelle doit
être fait et il est possible durant une phase d'amélioration d'altérer la
conformité d'autres arcs à cause d'un
![]() trop grand. Une étude plus approfondie est donc nécessaire pour
évaluer le nombre d'opérations effectuées par la méthode de mise
à l'échelle dans une configuration temps réel.
trop grand. Une étude plus approfondie est donc nécessaire pour
évaluer le nombre d'opérations effectuées par la méthode de mise
à l'échelle dans une configuration temps réel.
|