|
5. TENSION DANS UN GRAPHE SERIE-PARALLELE |
Au cours de notre introduction aux problématiques de synchronisation, nous avons souligné les différentes contraintes que les auteurs de documents hypermédia souhaitent utiliser (cf. section 1.1). Mais dans la première partie de notre étude, nous avons complètement éludé la nature même de ces contraintes et avons travaillé sur des graphes complètement aléatoires.
La raison de cette démarche est que nous ne pouvons pas nous limiter à l'étude de petits graphes, bien que les utilisateurs de ces systèmes synchronisés nous garantissent actuellement qu'une centaine de noeuds c'est déjà beaucoup. En effet, si des systèmes efficaces de synchronisation hypermédia sont mis en place dans les années à venir, les utilisateurs ne se contenteront plus de petits documents mais tenteront de synchroniser des documents pouvant se modéliser par des graphes avec probablement plusieurs milliers de noeuds. Cependant, nous ne disposons que de très peu d'exemples et aucun de grande taille. Il nous faut donc les générer. Mais ne voulant pas créer des graphes plus simples que ceux que proposeraient les concepteurs de documents synchronisés, nous avons pensé que générer des graphes totalement quelconques serait la meilleure manière d'éviter l'introduction d'un biais dans nos résultats.
Dans ce chapitre, nous proposons de considérer la nature particulière des contraintes de synchronisation. Nous verrons qu'une classe de graphes, les graphes série-parallèles, modélise des synchronisations très proches des exigences des auteurs de documents hypermédia, dans la limite de ce qu'un graphe temporel peut modéliser. Il faut noter que la résolution d'un problème d'optimisation sur ce genre de graphe est souvent plus simple que sur un graphe quelconque (e.g. [Datta99], [Baiou97], [Bern87], [Takamizawa82]).
La première partie de ce chapitre sera tout naturellement consacrée à la présentation de ces graphes très particuliers, aux limitations qu'ils apportent par rapport aux cas réels de synchronisation hypermédia et comment les détecter. Ensuite, nous proposons une méthode appelée agrégation qui exploite pleinement la structure particulière des graphes série-parallèles. Nous comparons alors cet algorithme avec les méthodes présentées au chapitre précédent pour la résolution du problème de tension de coût minimal sur des graphes série-parallèles (nous nous limitons à des coûts convexes linéaires par morceaux, cf. figure 2.11b).
Aux vues de l'efficacité de la méthode d'agrégation, nous avons pensé l'exploiter pour résoudre le problème de tension de coût minimal sur des graphes quelconques. Pour cela, nous proposons de décomposer les graphes en sous-graphes série-parallèles, appelés composantes série-parallèles et de résoudre le problème sur ces sous-graphes, avant de rassembler les composantes. L'idée ici étant que pour des cas réels de synchronisation hypermédia, les graphes seront presque série-parallèles.
| 5.1. SERIE-PARALLELE |
Dans cette section, nous présentons la classe des graphes série-parallèles et leurs principales caractéristiques. Nous verrons que la structure récursive de ces graphes peut être représentée par un arbre binaire qui nous facilitera par la suite la conception d'algorithmes. Enfin, nous discutons et justifions quelques méthodes pour identifier un graphe série-parallèle et construire sa représentation sous forme d'arbre.
| 5.1.1. Graphe série-parallèle, SP-graphe |
Il est possible de définir un graphe série-parallèle de plusieurs manières. Nous avons choisi une définition couramment employée (e.g. [Duffin65], [Eppstein92], [Valdes82]) qui repose sur une construction récursive du graphe très intuitive et très proche de la manière de créer des contraintes de synchronisation dans un document hypermédia.
| 5.1.1.1. Définition récursive |
Un graphe est dit série-parallèle s'il est obtenu à partir d'un graphe à deux sommets reliés par un seul arc, en appliquant récursivement les deux opérations suivantes.
L'opération série, appelée aussi sérialisation, consiste à insérer un nouveau sommet de degrés entrant et sortant égaux à
 en divisant un arc donné du graphe.
en divisant un arc donné du graphe. 
Figure 5.1: Opération série. Cette opération, que l'on notera
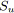 quand elle est appliquée à un arc
quand elle est appliquée à un arc
 , associe une relation notée
, associe une relation notée
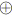 entre deux arcs nouvellement créés. Ainsi, l'opération
entre deux arcs nouvellement créés. Ainsi, l'opération
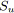 remplace
remplace
 par deux arcs,
par deux arcs,
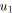 et
et
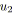 par exemple, et elle associe
par exemple, et elle associe
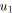 et
et
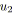 dans une relation série notée
dans une relation série notée
 .
.
-
L'opération parallèle, appelée aussi parallélisation, consiste à dupliquer un arc donné entre deux sommets.
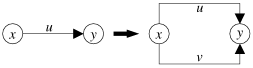
Figure 5.2: Opération parallèle. Cette opération, que l'on notera
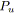 quand elle est appliquée à un arc
quand elle est appliquée à un arc
 , associe une relation notée
, associe une relation notée
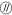 entre l'arc
entre l'arc
 et l'arc dupliqué. Ainsi, l'opération
et l'arc dupliqué. Ainsi, l'opération
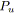 crée un nouvel arc,
crée un nouvel arc,
 par exemple, et elle associe
par exemple, et elle associe
 et
et
 dans une relation parallèle notée
dans une relation parallèle notée
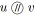 .
.
Par la suite, un graphe série-parallèle sera appelé SP-graphe, comme le propose par exemple [Ho99] (à ne pas confondre avec le même terme proposé dans [Schoenmakers95] pour des graphes série-parallèles sans arcs multiples, i.e. sans arcs avec la même origine et la même destination).
| 5.1.1.2. SP-relations |
Par la suite, nous regroupons les relations
![]() et
et
![]() définies précédemment sous le terme SP-relations. La
propriété suivante montre la corrélation qu'il existe entre le nombre d'arcs
et de noeuds d'un SP-graphe et le nombre de relations séries et parallèles qu'il
contient.
définies précédemment sous le terme SP-relations. La
propriété suivante montre la corrélation qu'il existe entre le nombre d'arcs
et de noeuds d'un SP-graphe et le nombre de relations séries et parallèles qu'il
contient.
Soit un SP-graphe, avec
et
. Il contient
relations séries et
relations parallèles. Par conséquent, il possède globalement
SP-relations.
(5.1)
Preuve:
Une opération série ajoute
![]() noeud à chaque application alors qu'une opération parallèle n'en
ajoute aucun. Le graphe de départ contenant
noeud à chaque application alors qu'une opération parallèle n'en
ajoute aucun. Le graphe de départ contenant
![]() noeuds, il faut
noeuds, il faut
![]() opérations séries pour construire le graphe final. De même, chaque
opération série ou parallèle ajoute
opérations séries pour construire le graphe final. De même, chaque
opération série ou parallèle ajoute
![]() arc. Comme le graphe de départ contient
arc. Comme le graphe de départ contient
![]() arc et qu'il y a
arc et qu'il y a
![]() arcs créés par les opérations séries, il faut
arcs créés par les opérations séries, il faut
![]() opérations parallèles.
opérations parallèles.
![]()
| 5.1.1.3. Tension principale |
D'après la définition d'un SP-graphe proposée précédemment,
il est très facile de vérifier qu'il contient un seul noeud source (i.e. ne
possédant aucun prédécesseur) et un seul noeud puits (i.e. ne
possédant aucun successeur). Soit une tension
![]() sur un SP-graphe
sur un SP-graphe
![]() , on appelle tension principale et on note
, on appelle tension principale et on note
![]() la tension entre le noeud source et le noeud puits de
la tension entre le noeud source et le noeud puits de
![]() .
.
| 5.1.2. Arbre binaire de décomposition, SP-arbre |
Les SP-graphes ayant une structure récursive très particulière, il est intéressant, pour un développement plus aisé d'algorithmes efficaces, de représenter ces graphes sous une forme plus adaptée à leur structure. Nous montrons tout d'abord comment modéliser ces graphes sous forme d'expression de SP-relations. Ensuite, nous proposons une représentation équivalente par un arbre binaire.
| 5.1.2.1. Représentation sous forme d'expression |
Revenons à la définition d'un SP-graphe. Ce dernier est créé en
appliquant une opération série ou parallèle sur l'un des arcs du graphe
à chaque itération du processus de construction. Considérons tout d'abord la
première itération, le graphe se limite à un simple arc
![]() (cf. figure 5.3a).
(cf. figure 5.3a).
 |
| Figure 5.3: Un exemple de construction d'un SP-graphe. |
L'opération
![]() ou
ou
![]() est alors appliquée, à l'itération
est alors appliquée, à l'itération
![]() le graphe possède donc deux arcs qui sont liés soit par la relation
série
le graphe possède donc deux arcs qui sont liés soit par la relation
série
![]() , soit par la relation parallèle
, soit par la relation parallèle
![]() . Supposons l'opération parallèle, à l'itération
. Supposons l'opération parallèle, à l'itération
![]() le graphe est donc
le graphe est donc
![]() (cf. figure 5.3b). L'un des deux arcs subit ensuite une autre opération
série ou parallèle, disons l'opération
(cf. figure 5.3b). L'un des deux arcs subit ensuite une autre opération
série ou parallèle, disons l'opération
![]() . Le graphe est alors
. Le graphe est alors
![]() (cf. figure 5.3c). On peut ainsi en déduire la propriété
suivante.
(cf. figure 5.3c). On peut ainsi en déduire la propriété
suivante.
Un SP-graphe peut toujours être représenté par une expression de SP-relations qui n'est pas toujours unique. (5.2)
Preuve:
Nous avons vu qu'en suivant la construction d'un SP-graphe, on peut toujours écrire une
expression de SP-relations le représentant. Poursuivons notre exemple en ajoutant
l'opération
![]() . On obtient alors le graphe
. On obtient alors le graphe
![]() (cf. figure 5.3d). Supposons maintenant la construction
(cf. figure 5.3d). Supposons maintenant la construction
![]() illustrée par la figure 5.4, on obtient alors l'expression
illustrée par la figure 5.4, on obtient alors l'expression
![]() qui représente un graphe identique à celui obtenu dans notre premier
exemple de construction.
qui représente un graphe identique à celui obtenu dans notre premier
exemple de construction.
![]()
 |
| Figure 5.4: Un autre exemple de construction d'un SP-graphe. |
Nous avons défini une SP-relation comme étant une relation entre deux arcs. Cependant, d'après le principe de construction d'un SP-graphe, on s'aperçoit que ces relations, au départ établies entre deux arcs, deviennent au cours du processus de construction des relations entre sous-graphes (car un arc peut être remplacé à tout moment par une SP-relation). Ainsi, on introduit la notion de SP-relation simple pour désigner une SP-relation entre deux arcs. Lors de la construction d'un SP-graphe, la dernière opération série ou parallèle crée forcément une SP-relation simple, ce qui nous permet d'affirmer la propriété suivante qui nous sera très utile par la suite.
Un SP-graphe possède au moins une SP-relation simple. (5.3)
| 5.1.2.2. Représentation sous forme d'arbre |
Les SP-relations sont binaires, il est donc très facile et immédiat de
représenter l'expression d'un SP-graphe par un arbre binaire que certains appellent arbre
binaire de décomposition (e.g. [Valdes82],
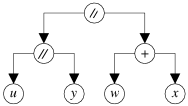
[Datta99]), et d'autres SP-arbre (e.g. [Bodlaender96]). La figure 5.5 illustre cette représentation pour
l'expression
![]() de l'exemple précédent.
de l'exemple précédent.
|
|
Nous proposons ici une définition équivalente de l'arbre binaire de décomposition qui met en évidence la relation qu'il existe entre un sous-arbre d'un SP-arbre et un sous-graphe du SP-graphe associé.
|
|
Voici la définition récursive d'un SP-arbre.
- Le SP-arbre représentant un SP-graphe avec seulement un arc reliant deux sommets est formé d'un seul noeud qui représente l'unique arc du graphe (cf. figure 5.6).
- Un SP-arbre représentant un SP-graphe avec au moins une SP-relation est formé d'un noeud racine représentant une SP-relation et de deux SP-arbres représentant les deux sous-graphes impliqués dans la relation en question (cf. figures 5.7 et 5.8).
En résumé, il est toujours possible de représenter un SP-graphe par une expression de SP-relations ou par un SP-arbre, mais partant d'un SP-graphe déjà construit, il est souvent possible de trouver plusieurs représentations. Pour obtenir une représentation unique, il suffit de considérer les SP-relations non plus binaires mais s'appliquant à un nombre quelconque d'arcs ou de sous-graphes (cf. [Bodlaender96]). Dans notre utilisation de cette représentation, la pluralité des représentations ne pose aucun problème.
| 5.1.3. Opérateurs de synchronisation série-parallèles |
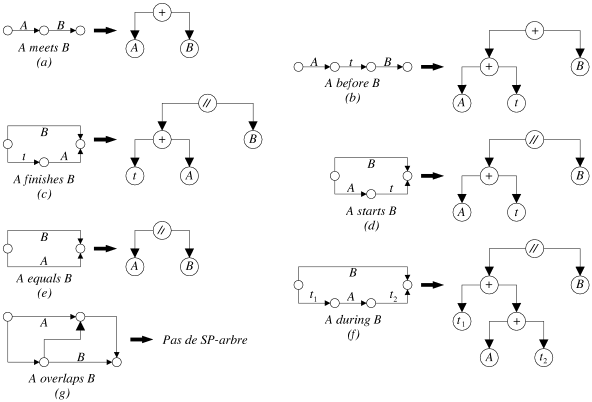 |
| Figure 5.9: SP-arbres des opérateurs de synchronisation, partie 1. |
Dans le chapitre 2, nous avons présenté les limites qu'une modélisation sous forme de graphe implique aux contraintes de synchronisation d'un document hypermédia. Parmi tous les opérateurs préconisés dans [Jourdan99], nous n'en avons retenu qu'une partie résumée par la figure 1.2 (les opérateurs de l'algèbre de Allen proposée dans [Allen83] et leurs principales disjonctions). Nous proposons d'identifier ici les opérateurs qui ont une représentation série-parallèle, afin de mieux juger de la pertinence d'une restriction de la modélisation des contraintes de synchronisation à un SP-graphe. La figure 5.9 montre le SP-arbre (quand cela est possible) associé à chaque opérateur retenu au chapitre 2.
Nous avons volontairement écarté les opérateurs share-start et
share-end de cette première analyse, puisqu'ils ne peuvent pas être
représentés par des SP-graphes. Cependant ils peuvent tout de même être
utilisés dans un graphe des contraintes série-parallèle. En effet, n'oublions
pas que ce graphe est temporel, ce qui signifie qu'il possède un seul noeud source et un
seul noeud puits. Ainsi, pour l'opérateur share-start par exemple, les
scénarios
![]() et
et
![]() lancés en parallèle se rencontrent forcément à un moment
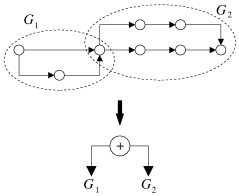
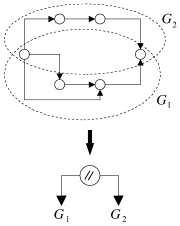
ou à un autre comme le montre la figure 5.10a. En supposant que les sous-graphes
lancés en parallèle se rencontrent forcément à un moment
ou à un autre comme le montre la figure 5.10a. En supposant que les sous-graphes
![]() et
et
![]() sont série-parallèles, il est facile de vérifier que le graphe
est série-parallèle (cf. figure 5.10b). Le même raisonnement peut être
appliqué à l'opérateur share-end.
sont série-parallèles, il est facile de vérifier que le graphe
est série-parallèle (cf. figure 5.10b). Le même raisonnement peut être
appliqué à l'opérateur share-end.
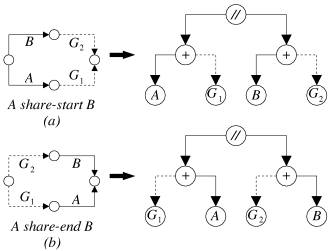 |
| Figure 5.10: SP-arbres des opérateurs de synchronisation, partie 2. |
Finalement, en n'utilisant que des opérateurs (y compris les SP-relations) avec une représentation série-parallèle pour construire le graphe des contraintes, on obtient forcément un SP-graphe. Se limiter à ces opérateurs n'est pas si restrictif, puisque seul l'opérateur overlaps, parmi tous ceux modélisables par un graphe temporel, n'est pas représentable par un SP-graphe, et ce n'est apparemment pas le plus important.
| 5.1.4. Construction d'un SP-arbre |
Le problème de reconnaître un SP-graphe est connu depuis longtemps comme étant un problème facile qui peut être résolu en temps linéaire (cf. [Valdes82]). Les différents algorithmes proposés dans la littérature peuvent être adaptés très facilement et sans altération de leur complexité pour construire le SP-arbre au moment de la reconnaissance. Ces méthodes étant très efficaces, notre discussion ne portera pas ici sur leur complexité, mais plutôt sur leur manière d'aborder le problème et de reconnaître un SP-graphe. Car dans la seconde partie du chapitre, nous ne nous contenterons pas seulement d'identifier un SP-graphe, mais nous tenterons d'extraire des composantes série-parallèles de graphes quelconques. Afin de les adapter à cet objectif, nous présentons les deux approches que nous avons retenues de la littérature et de nos propres réflexions: l'approche par réduction et l'approche par chemin.
Une petite remarque tout de même sur la complexité de ces méthodes. Les
auteurs affirment que leur complexité est linéaire, c'est-à-dire en
![]() opérations dans [Valdes82]. Il faut noter que cela
est vrai seulement avec une structure de graphe particulière qui est souvent passée
sous silence. Cependant, vue l'efficacité des méthodes proposées, il faut
s'inquiéter du temps de construction de cette structure. Dans [Schoenmakers95] par exemple, il s'agit d'une matrice d'adjacence noeud-noeud
qui nécessite donc
opérations dans [Valdes82]. Il faut noter que cela
est vrai seulement avec une structure de graphe particulière qui est souvent passée
sous silence. Cependant, vue l'efficacité des méthodes proposées, il faut
s'inquiéter du temps de construction de cette structure. Dans [Schoenmakers95] par exemple, il s'agit d'une matrice d'adjacence noeud-noeud
qui nécessite donc
![]() opérations pour être construite. Dans [Valdes82], identifier si un arc possède un double (i.e. un arc avec
même origine et même destination) est effectué en
opérations pour être construite. Dans [Valdes82], identifier si un arc possède un double (i.e. un arc avec
même origine et même destination) est effectué en
![]() opérations, ce qui est possible seulement après un tri des arcs entrants
et sortants de chaque noeud et nécessite
opérations, ce qui est possible seulement après un tri des arcs entrants
et sortants de chaque noeud et nécessite
![]() opérations. Le calcul de la complexité des méthodes que nous
présentons ici (et même ailleurs dans le document) considère une structure de
données raisonnablement efficace, mais sans artifice particulier.
opérations. Le calcul de la complexité des méthodes que nous
présentons ici (et même ailleurs dans le document) considère une structure de
données raisonnablement efficace, mais sans artifice particulier.
Pour les besoins de nos algorithmes, nous avons choisi une notation récursive des arbres
binaires (cf. chapitre 2). Nous rappelons seulement qu'un arbre de racine
![]() , de sous-arbre gauche
, de sous-arbre gauche
![]() et de sous-arbre droit
et de sous-arbre droit
![]() sera noté
sera noté
![]() . Nous introduisons également ci-dessous les procédures inverses des
opérations série et parallèle, appelées SP-réductions.
. Nous introduisons également ci-dessous les procédures inverses des
opérations série et parallèle, appelées SP-réductions.
- La réduction série, notée
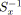 , remplace la SP-relation
, remplace la SP-relation
 par un arc
par un arc
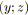 .
.
- La réduction parallèle, notée
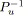 , remplace la SP-relation
, remplace la SP-relation
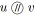 par l'arc
par l'arc
 .
.
| 5.1.4.1. Approche par réduction |
Cette première approche est la plus répandue, car la plus intuitive. Elle repose sur un constat évident que nous avons établi précédemment: un graphe série-parallèle possède au moins une SP-relation simple. L'idée est donc d'identifier une telle relation et d'appliquer la réduction correspondant, afin de remonter le processus de construction du SP-graphe.
Cette méthode a tout d'abord été proposée dans [Valdes82]. On la retrouve ensuite dans [Schoenmakers95] avec une petite amélioration: au départ tous
les arcs multiples sont éliminés (il n'existe donc plus de relations
parallèles simples), ensuite on détecte les relation séries et des relations
parallèles-et-séries (composition d'une relation parallèle avec une
relation série:
![]() ). La détection est alors plus facile (on regarde uniquement les noeuds) et la
réduction est plus efficace puisque dans le cas d'une relation
parallèle-et-série, deux arcs et un noeud sont éliminés par rapport
à une relation parallèle qui ne supprime qu'un seul arc. Cependant, nous ne retenons
pas cette amélioration, puisque fondamentalement elle ne change pas l'approche et se
prête difficilement à notre soucis futur qui est d'extraire les composantes
série-parallèles d'un graphe quelconque. Une variante similaire a également
été proposée dans [Bodlaender96] qui offre 18
réductions, cependant la plupart ne sont valables que pour un graphe non orienté.
). La détection est alors plus facile (on regarde uniquement les noeuds) et la
réduction est plus efficace puisque dans le cas d'une relation
parallèle-et-série, deux arcs et un noeud sont éliminés par rapport
à une relation parallèle qui ne supprime qu'un seul arc. Cependant, nous ne retenons
pas cette amélioration, puisque fondamentalement elle ne change pas l'approche et se
prête difficilement à notre soucis futur qui est d'extraire les composantes
série-parallèles d'un graphe quelconque. Une variante similaire a également
été proposée dans [Bodlaender96] qui offre 18
réductions, cependant la plupart ne sont valables que pour un graphe non orienté.
Nous présentons donc ici une version générique de la méthode, en
construisant en même temps un SP-arbre représentant le supposé SP-graphe. Pour
cela, on introduit la fonction
![]() qui associe un SP-arbre
qui associe un SP-arbre
![]() à chaque arc
à chaque arc
![]() du graphe
du graphe
![]() . Au départ, chaque arc possède un SP-arbre avec un seul noeud qui est
l'arc lui-même. Voici ce qui se produit lors d'une réduction.
. Au départ, chaque arc possède un SP-arbre avec un seul noeud qui est
l'arc lui-même. Voici ce qui se produit lors d'une réduction.
- La réduction série
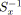 supprime les deux arcs
supprime les deux arcs
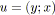 et
et
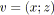 de la relation
de la relation
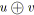 , et crée un arc
, et crée un arc
 . Le SP-arbre de
. Le SP-arbre de
 est alors
est alors
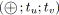 .
.
- La réduction parallèle
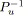 supprime l'arc
supprime l'arc
 de la relation
de la relation
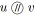 . Le SP-arbre de
. Le SP-arbre de
 devient alors
devient alors
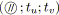 .
.
L'algorithme 5.1 décrit toute la procédure de reconnaissance d'un SP-graphe et la construction de son SP-arbre. Il est facile de vérifier qu'à chaque réduction, si le graphe est série-parallèle, il le reste et que par conséquent il existe toujours au moins une SP-relation simple. En revanche, si le graphe n'est pas série-parallèle, il y aura une réduction après laquelle il n'y aura plus de SP-relation simple. Ainsi, si l'algorithme parvient à réduire un graphe à un seul arc, alors le SP-arbre associé à l'arc représente le SP-graphe initial. Sinon, cela signifie que le graphe n'était pas série-parallèle.
Algorithme 5.1: construireSPArbre(graphe
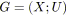 ,arbre
,arbre
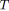 )
)
pour tout
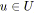 faire
faire


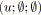 ;
;
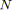

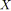 ;
; 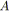

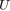 ;
;
tant que
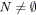 faire
faire
/* Réductions séries. */
tant que
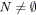 faire
faire
choisir
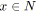 ;
; 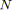

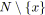 ;
;
si
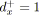 et
et
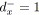 alors
alors
soit
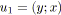 et
et
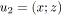
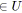 ;
;


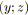 ;
;


 ;
;
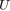

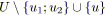 ;
;
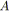

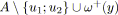 ;
;
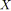

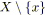 ;
;
fin si;
fin tant que;
/* Réductions parallèles. */
tant que
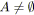 faire
faire
choisir
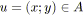 ;
; 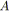

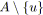 ;
;
tant que
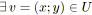 tel que
tel que
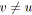 faire
faire


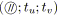 ;
;
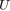

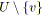 ;
; 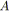

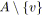 ;
;
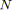

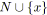 ;
; 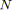

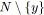 ;
;
fin tant que;
fin tant que;
fin tant que;
si
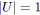 alors soit
alors soit
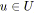 ;
;
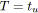 ;
;
sinon arrêter; /* Le graphe n'est pas
série-parallèle. */
fin algorithme; L'examination d'un noeud se fait en
![]() opérations et celle d'un arc en
opérations et celle d'un arc en
![]() (il faut regarder tous les arcs ayant la même origine). Au départ de
l'algorithme, tous les noeuds sont examinés ainsi que tous les arcs. La première
passe nécessite donc
(il faut regarder tous les arcs ayant la même origine). Au départ de
l'algorithme, tous les noeuds sont examinés ainsi que tous les arcs. La première
passe nécessite donc
![]() opérations. Ensuite, un noeud ne sera examiné qu'après une
réduction parallèle. De la même manière, un arc ne sera examiné
que suite à une réduction série. Sachant qu'il y a
opérations. Ensuite, un noeud ne sera examiné qu'après une
réduction parallèle. De la même manière, un arc ne sera examiné
que suite à une réduction série. Sachant qu'il y a
![]() relations série et
relations série et
![]() relations parallèles, les passes suivantes de l'algorithme nécessitent
relations parallèles, les passes suivantes de l'algorithme nécessitent
![]() opérations. Enfin, une SP-réduction consiste en l'agrégation d'un
SP-arbre,
opérations. Enfin, une SP-réduction consiste en l'agrégation d'un
SP-arbre,
![]() opérations, et en la suppression d'un noeud ou d'un arc (le nombre
d'opérations ici est fortement dépendant de la structure employée pour
représenter le graphe, une structure raisonnable nécessite au pire
opérations, et en la suppression d'un noeud ou d'un arc (le nombre
d'opérations ici est fortement dépendant de la structure employée pour
représenter le graphe, une structure raisonnable nécessite au pire
![]() opérations). Sachant qu'il y a au plus
opérations). Sachant qu'il y a au plus
![]() SP-relations, les réductions coûtent
SP-relations, les réductions coûtent
![]() opérations. Au final, l'algorithme nécessite donc
opérations. Au final, l'algorithme nécessite donc
![]() opérations.
opérations.
| 5.1.4.2. Approche par chemin |
L'approche que nous proposons ici est plus globale que celle présentée précédemment. Visuellement, il est relativement facile d'identifier un SP-graphe. La raison est simplement que les chemins d'un tel graphe sont organisés de manière très particulière. Dans [Eppstein92], cette organisation est formalisée par le concept de décomposition en oreille (ear decomposition). Notre intérêt portera plutôt sur deux types de noeuds jouant un rôle très particulier: les noeuds de branchement (dont le degré sortant est supérieur à 1) et les noeuds de synchronisation (dont le degré entrant est supérieur à 1).
Dans un graphe série-parallèle, de tels noeuds représentent respectivement le début et la fin de SP-relations parallèles. On nomme branchement deux arcs sortants d'un noeud de branchement (i.e. le début d'une SP-relation parallèle). De même, une synchronisation représente deux arcs entrants d'un noeud de synchronisation (i.e. la fin d'une SP-relation parallèle). Par simplicité, on pourra parfois confondre le branchement (respectivement la synchronisation) avec son noeud de branchement (respectivement de synchronisation).
 |
| Figure 5.11: Un exemple de branchements. |
L'approche proposée ici est basée sur un parcours du graphe dans un ordre
topologique (i.e. un noeud est visité après tous ses prédécesseurs).
Notons
![]() l'ensemble des noeuds marqués par le parcours du graphe à
l'itération
l'ensemble des noeuds marqués par le parcours du graphe à
l'itération
![]() . Un branchement
. Un branchement
![]() est dit fermé à l'itération
est dit fermé à l'itération
![]() s'il existe un noeud de synchronisation
s'il existe un noeud de synchronisation
![]() tel qu'il existe deux chemins
tel qu'il existe deux chemins
![]() et
et
![]() entre
entre
![]() et
et
![]() distincts (i.e. n'ayant aucun arc en commun), et contenant chacun l'un des deux arcs du
branchement; les deux arcs entrants de
distincts (i.e. n'ayant aucun arc en commun), et contenant chacun l'un des deux arcs du
branchement; les deux arcs entrants de
![]() appartenant chacun à l'un des chemins forment alors une synchronisation
appartenant chacun à l'un des chemins forment alors une synchronisation
![]() . Un branchement non fermé est dit ouvert. On dit également que la
synchronisation
. Un branchement non fermé est dit ouvert. On dit également que la
synchronisation
![]() ferme le branchement
ferme le branchement
![]() . A un branchement fermé, on associera une synchronisation particulière,
qui est la première synchronisation qui ferme le branchement dans le parcours topologique.
Les chemins qui permettent la fermeture du branchement (dans la définition
. A un branchement fermé, on associera une synchronisation particulière,
qui est la première synchronisation qui ferme le branchement dans le parcours topologique.
Les chemins qui permettent la fermeture du branchement (dans la définition
![]() et
et
![]() ) seront appelés par la suite chemins de fermeture.
) seront appelés par la suite chemins de fermeture.
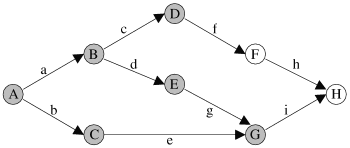
 |
| Figure 5.12: Un exemple de branchement ouvert sur un chemin de fermeture. |
Pour illustrer ces définitions, considérons la figure 5.11. Les noeuds
grisés représentent ceux visités à une itération donnée
![]() .
.
![]() et
et
![]() sont des noeuds de branchement,
sont des noeuds de branchement,
![]() et
et
![]() des noeuds de synchronisation.
des noeuds de synchronisation.
![]() est un branchement fermé à l'itération
est un branchement fermé à l'itération
![]() , la synchronisation associée étant
, la synchronisation associée étant
![]() . En revanche, le branchement
. En revanche, le branchement
![]() est ouvert à l'itération
est ouvert à l'itération
![]() . Les chemins de fermeture du branchement
. Les chemins de fermeture du branchement
![]() sont
sont
![]() et
et
![]() . Le graphe de notre exemple n'est pas série-parallèle. Intuitivement, on
s'aperçoit que le problème vient du branchement ouvert
. Le graphe de notre exemple n'est pas série-parallèle. Intuitivement, on
s'aperçoit que le problème vient du branchement ouvert
![]() . Tentons alors de prouver la proposition suivante.
. Tentons alors de prouver la proposition suivante.
Un graphe est série-parallèle si et seulement si, à toute itération du parcours et pour tout branchement fermé, il existe deux chemins de fermeture entre le branchement
et la synchronisation associée
qui ne possèdent pas de branchement ouvert.
(5.4)
Preuve:
(![]() ) A une itération donnée, s'il existe un branchement
) A une itération donnée, s'il existe un branchement
![]() ouvert sur l'un des chemins de fermeture d'un branchement fermé
ouvert sur l'un des chemins de fermeture d'un branchement fermé
![]() associé à une synchronisation
associé à une synchronisation
![]() , cela donne un graphe dont l'allure générale est présentée
par la figure 5.12a (les noeuds grisés représentent ceux visités). En tentant
une réduction par l'algorithme 5.1, cela aboutit au mieux au graphe illustré par la
figure 5.12b. La réduction ne peut donc pas se terminer, le graphe n'est donc pas
série-parallèle.
, cela donne un graphe dont l'allure générale est présentée
par la figure 5.12a (les noeuds grisés représentent ceux visités). En tentant
une réduction par l'algorithme 5.1, cela aboutit au mieux au graphe illustré par la
figure 5.12b. La réduction ne peut donc pas se terminer, le graphe n'est donc pas
série-parallèle.
(![]() ) La preuve de cette implication peut être faite par la justification de
l'algorithme 5.4 présenté dans la suite de cette section. En effet, ce dernier
construit un SP-arbre associé à un graphe en vérifiant que tout branchement
fermé ne possède pas de branchement ouvert dans ses chemins de fermeture.
) La preuve de cette implication peut être faite par la justification de
l'algorithme 5.4 présenté dans la suite de cette section. En effet, ce dernier
construit un SP-arbre associé à un graphe en vérifiant que tout branchement
fermé ne possède pas de branchement ouvert dans ses chemins de fermeture.
![]()
Pour vérifier la proposition 5.4 (afin de déterminer si un graphe est
série-parallèle), on propose un système de marquage qui permet
d'établir, à l'arrivée sur une synchronisation, les branchements qui se
ferment et si un branchement ouvert est présent sur les chemins de fermeture. On note
![]() la signature d'un arc
la signature d'un arc
![]() , elle se résume à un noeud de branchement.
, elle se résume à un noeud de branchement.
![]() signifie que
signifie que
![]() est le dernier (par rapport à l'ordre topologique) branchement non fermé
sur les chemins entre la source et l'arc
est le dernier (par rapport à l'ordre topologique) branchement non fermé
sur les chemins entre la source et l'arc
![]() . On note également
. On note également
![]() la signature d'un noeud
la signature d'un noeud
![]() , elle consiste en un couple
, elle consiste en un couple
![]() . Si le noeud n'est pas un noeud de branchement alors
. Si le noeud n'est pas un noeud de branchement alors
![]() , sinon
, sinon
![]() indique le nombre de branchements de noeud
indique le nombre de branchements de noeud
![]() ouverts.
ouverts.
![]() indique le niveau du branchement, e.g. si
indique le niveau du branchement, e.g. si
![]() , alors il existe deux branchements ouverts dans les chemins entre la source et
, alors il existe deux branchements ouverts dans les chemins entre la source et
![]() (
(![]() compris).
compris).
La signature d'un arc ou d'un noeud n'est pas définitive, elle peut changer au cours du
parcours topologique. En effet, lorsque deux arcs
![]() et
et
![]() de même signature
de même signature
![]() (à l'itération
(à l'itération
![]() ) se rejoignent à un noeud de synchronisation
) se rejoignent à un noeud de synchronisation
![]() (à l'itération
(à l'itération
![]() ), ils forment une synchronisation et ferment donc un branchement de noeud
), ils forment une synchronisation et ferment donc un branchement de noeud
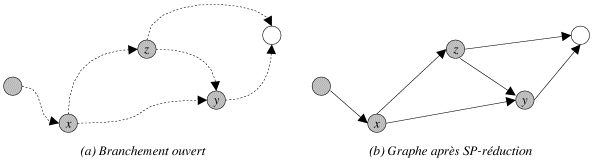
![]() (cf. figure 5.13a). La signature de leur branchement
(cf. figure 5.13a). La signature de leur branchement
![]() est alors modifiée:
est alors modifiée:
![]() est décrémenté de
est décrémenté de
![]() . Si
. Si
![]() atteint alors
atteint alors
![]() , cela signifie que tous les branchements de noeud
, cela signifie que tous les branchements de noeud
![]() sont fermés. La signature des arcs
sont fermés. La signature des arcs
![]() et
et
![]() doit changer, elle devient le branchement ouvert avant
doit changer, elle devient le branchement ouvert avant
![]() , i.e. la signature du ou des arcs entrants au branchement
, i.e. la signature du ou des arcs entrants au branchement
![]() (cf. figure 5.13b). Idéalement il faudrait changer la signature de tous les arcs
de signature
(cf. figure 5.13b). Idéalement il faudrait changer la signature de tous les arcs
de signature
![]() , mais pour les besoins de l'algorithme (qui n'effectue qu'un parcours topologique et ne
revient donc pas sur des arcs déjà utilisés) cette modification n'est pas
nécessaire.
, mais pour les besoins de l'algorithme (qui n'effectue qu'un parcours topologique et ne
revient donc pas sur des arcs déjà utilisés) cette modification n'est pas
nécessaire.
 |
| Figure 5.13: Un exemple de changement de signature. |
L'algorithme 5.2 proposé effectue un parcours topologique du graphe, en marquant
progressivement les arcs et les noeuds de la signature
![]() . Il est supposé que le graphe n'a qu'une seule source et au moins un arc, sinon
il est certain qu'il n'est pas série-parallèle. Partant de la source, l'algorithme va
ainsi marquer les noeuds et les arcs du graphe. A chaque noeud de synchronisation
. Il est supposé que le graphe n'a qu'une seule source et au moins un arc, sinon
il est certain qu'il n'est pas série-parallèle. Partant de la source, l'algorithme va
ainsi marquer les noeuds et les arcs du graphe. A chaque noeud de synchronisation
![]() , il se charge de modifier certaines signatures pour représenter la fermeture de
branchements associés (cf. algorithme 5.3). Si à la fin de cette étape, deux
arcs entrants
, il se charge de modifier certaines signatures pour représenter la fermeture de
branchements associés (cf. algorithme 5.3). Si à la fin de cette étape, deux
arcs entrants
![]() et
et
![]() n'ont pas la même signature, cela signifie que le graphe n'est pas
série-parallèle.
n'ont pas la même signature, cela signifie que le graphe n'est pas
série-parallèle.
Algorithme 5.2: détecterSPGraphe(graphe
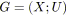 )
)
pour tout
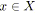 faire
faire
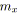

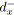 ; /* Marque pour le parcours
topologique. */
; /* Marque pour le parcours
topologique. */
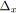

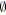 ; /* Permet de savoir si un noeud a
été visité. */
; /* Permet de savoir si un noeud a
été visité. */
fin pour;
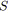

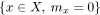 ;
;
si
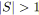 ou
ou
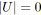 alors arrêter;
alors arrêter;
/* Le graphe n'est pas série-parallèle. */
tant que
 faire
faire
choisir
 dans
dans
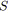 ;
;
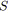

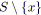 ;
;
si
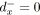 alors
alors
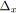

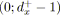 ;
;
sinon
si
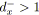 alors fermerBranchements(
alors fermerBranchements( ,
,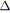 );
);
soit
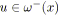 ;
; 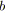

 ;
;
si
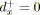 et
et
 alors /* Plusieurs noeuds puits. */
alors /* Plusieurs noeuds puits. */
arrêter; /* Le graphe n'est pas
série-parallèle. */
si
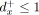 alors
alors
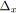

 ;
;
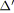

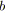 ;
;
sinon
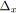

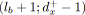 ;
;
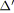

 ;
;
fin si;
pour tout
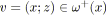 faire
faire
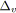

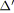 ;
;
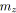

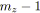 ;
;
si
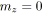 alors
alors
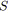

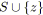 ;
;
fin pour;
fin si;
fin tant que;
si
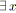 tel que
tel que
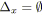 alors
alors
/* Un circuit a stoppé le parcours topologique. */
arrêter; /* Le graphe n'est pas
série-parallèle. */
sinon /* Le graphe est série-parallèle. */
fin algorithme; En effet, il existe deux chemins
![]() et
et
![]() entre la source et respectivement
entre la source et respectivement
![]() et
et
![]() . Ces chemins ont au moins un noeud de branchement en commun (au moins la source).
Considérons
. Ces chemins ont au moins un noeud de branchement en commun (au moins la source).
Considérons
![]() le dernier noeud (dans le parcours topologique) vérifiant cette condition. S'il
n'y avait pas de branchement ouvert sur les chemins de fermeture entre
le dernier noeud (dans le parcours topologique) vérifiant cette condition. S'il
n'y avait pas de branchement ouvert sur les chemins de fermeture entre
![]() et
et
![]() ,
,
![]() et
et
![]() auraient la même signature
auraient la même signature
![]() ; s'ils ne l'ont pas, cela signifie qu'au moins un des chemins de fermeture entre
; s'ils ne l'ont pas, cela signifie qu'au moins un des chemins de fermeture entre
![]() et
et
![]() possède un branchement ouvert dont
possède un branchement ouvert dont
![]() ou
ou
![]() portent la signature.
portent la signature.
Algorithme 5.3: fermerBranchements(noeud
 ,signature
,signature
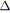 )
)
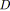

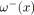 ;
;
trier
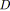 dans l'ordre décroissant des signatures;
dans l'ordre décroissant des signatures;
tant que
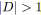 faire
faire
soit
 et
et
 les deux premiers arcs de
les deux premiers arcs de
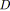 ;
;
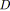

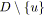 ;
;
si
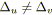 alors arrêter; /* Le graphe n'est pas
série-parallèle. */
alors arrêter; /* Le graphe n'est pas
série-parallèle. */


 ;
;
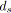

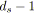 ;
;
si
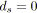 alors
alors
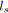

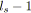 ;
;
soit
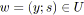 ;
;
pour tout
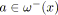 tel que
tel que
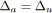 faire
faire
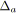

 ;
;
trier
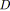 dans l'ordre décroissant des signatures;
dans l'ordre décroissant des signatures;
fin si;
fin tant que;
fin algorithme; L'algorithme 5.3 est chargé de fermer les branchements à un noeud de
synchronisation donné
![]() , et de modifier les signatures en conséquence. Il doit donc vérifier la
signature des arcs entrants de
, et de modifier les signatures en conséquence. Il doit donc vérifier la
signature des arcs entrants de
![]() deux à deux, et s'ils ont une signature identique, fermer le branchement
correspondant s'il est ouvert. Pour un parcours efficace des arcs, nous proposons de les trier dans
un ensemble
deux à deux, et s'ils ont une signature identique, fermer le branchement
correspondant s'il est ouvert. Pour un parcours efficace des arcs, nous proposons de les trier dans
un ensemble
![]() , dans l'ordre décroissant de leur signature, i.e.
, dans l'ordre décroissant de leur signature, i.e.
![]() avant
avant
![]()
![]()
![]() (on suppose un ordre quelconque sur les noeuds, l'important étant que dans
l'ensemble
(on suppose un ordre quelconque sur les noeuds, l'important étant que dans
l'ensemble
![]() , tous les arcs de même signature soient côte-à-côte). Ainsi,
en étudiant les deux premiers arcs de
, tous les arcs de même signature soient côte-à-côte). Ainsi,
en étudiant les deux premiers arcs de
![]() , on considère le branchement de niveau le plus élevé qu'il faut
absolument fermer avant tout branchement de niveau inférieur. Cette procédure
effectue donc
, on considère le branchement de niveau le plus élevé qu'il faut
absolument fermer avant tout branchement de niveau inférieur. Cette procédure
effectue donc
![]() opérations. L'algorithme complet 5.2 nécessite
opérations. L'algorithme complet 5.2 nécessite
![]() opérations, puisqu'il effectue un simple parcours en appelant l'algorithme 5.3
à chaque noeud visité.
opérations, puisqu'il effectue un simple parcours en appelant l'algorithme 5.3
à chaque noeud visité.
L'algorithme 5.2 ne permet que la détection d'un graphe série-parallèle,
il est simple ensuite de l'adapter, sans altération de la complexité, pour qu'il
construise un SP-arbre associé. L'idée consiste à réduire le graphe par
une opération série à chaque fois qu'un noeud de degrés entrant et
sortant égaux à
![]() est visité. Lorsqu'un branchement est fermé, cela signifie qu'une
opération parallèle a été détectée, il suffit alors de la
réduire. Le SP-arbre est construit une fois tout le graphe visité (il se
réduira alors à un simple arc).
est visité. Lorsqu'un branchement est fermé, cela signifie qu'une
opération parallèle a été détectée, il suffit alors de la
réduire. Le SP-arbre est construit une fois tout le graphe visité (il se
réduira alors à un simple arc).
Algorithme 5.4: construireSPArbreBis(graphe
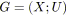 ,arbre
,arbre
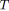 )
)
pour tout
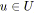 faire
faire


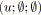 ;
;
pour tout
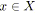 faire
faire
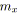

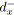 ;
;
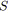

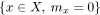 ;
;
tant que
 faire
faire
choisir
 dans
dans
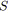 ;
;
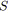

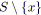 ;
;
si
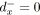 alors
alors
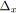

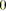 ;
;
sinon
si
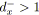 alors fermerBranchementsBis(
alors fermerBranchementsBis( ,
,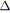 ,
,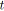 );
);
soit
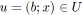 ;
;
si
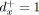 alors /* Réduction série. */
alors /* Réduction série. */
soit
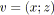
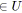 ;
;


 ;
;
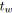

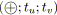 ;
;
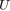

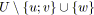 ;
;
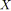

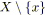 ;
;
sinon
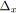

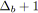 ;
;
pour tout
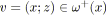 faire
faire
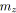

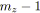 ;
;
si
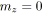 alors
alors
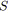

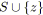 ;
;
fin pour;
fin si;
fin si;
fin tant que;
si
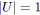 alors soit
alors soit
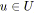 ;
;
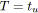 ;
;
sinon arrêter; /* Le graphe n'est pas
série-parallèle. */
fin algorithme; Nous proposons l'algorithme 5.4 accompagné de 5.5 qui permet une telle construction. La
gestion des signatures des arcs et des noeuds est plus simple avec cet algorithme, car les
SP-réductions déduisent automatiquement la plupart des signatures. En effet, la
signature
![]() d'un noeud
d'un noeud
![]() est limitée à
est limitée à
![]() (car
(car
![]() est toujours égal à
est toujours égal à
![]() ), et la signature d'un arc
), et la signature d'un arc
![]() n'est plus nécessaire, car elle est toujours égale à
n'est plus nécessaire, car elle est toujours égale à
![]() . Pour l'algorithme 5.1 (construction d'un SP-arbre par réduction), nous avons vu
que les réductions nécessitent
. Pour l'algorithme 5.1 (construction d'un SP-arbre par réduction), nous avons vu
que les réductions nécessitent
![]() opérations, l'algorithme 5.4 a donc la même complexité que
l'algorithme 5.2 de détection, autrement dit
opérations, l'algorithme 5.4 a donc la même complexité que
l'algorithme 5.2 de détection, autrement dit
![]() opérations.
opérations.
Algorithme 5.5: fermerBranchements(noeud
 ,signature
,signature
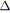 ,vecteur
,vecteur
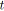 )
)
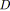

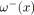 ;
;
trier
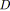 dans l'ordre décroissant des signatures;
dans l'ordre décroissant des signatures;
tant que
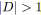 faire
faire
soit
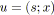 et
et
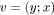 les deux premiers arcs de
les deux premiers arcs de
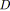 ;
;
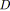

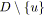 ;
;
si
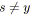 alors arrêter; /* Le graphe n'est pas
série-parallèle. */
alors arrêter; /* Le graphe n'est pas
série-parallèle. */
/* Réduction parallèle. */
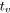

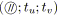 ;
;
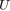

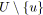 ;
;
si
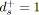 alors
alors
/* Réduction série. */
soit
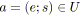 ;
;


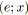 ;
;
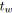

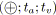 ;
;
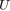

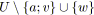 ;
;
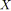

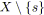 ;
;
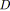

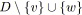 ;
;
trier
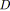 dans l'ordre décroissant des signatures;
dans l'ordre décroissant des signatures;
fin si;
fin tant que;
fin algorithme;
| 5.2. METHODE D'AGREGATION |
Nous proposons ici une méthode pour résoudre le problème de la tension de coût minimal sur des graphes série-parallèles (avec des coûts linéaires par morceaux, cf. 2.11b). Cette méthode est appelée agrégation car elle repose sur une approche qui consiste à remplacer récursivement une SP-relation par un seul arc aux propriétés équivalentes. Cette technique d'agrégation exploite la notion de fonction de coût minimal, que nous présentons avant de s'intéresser à l'agrégation d'une relation série, puis d'une relation parallèle. Nous expliquons enfin la méthode complète et la comparons aux méthodes présentées dans le chapitre précédent.
| 5.2.1. Fonction de coût minimal |
L'idée de la méthode d'agrégation consiste à remplacer un SP-graphe
par un arc, dit agrégé, aux propriétés équivalentes. Bien
évidemment, cette opération, appelée agrégation, élimine
certaines informations concernant le graphe pour n'en garder que les pertinentes pour le
problème qui nous intéresse, à savoir optimiser la tension du graphe. La
principale information agrégée que l'on considère tout d'abord est la
fonction de coût minimal d'un graphe
![]() , ou de son arc agrégé
, ou de son arc agrégé
![]() . Cette fonction, notée
. Cette fonction, notée
![]() , représente le coût minimal de la tension de
, représente le coût minimal de la tension de
![]() , pour une tension principale
, pour une tension principale
![]() forcée à une valeur donnée
forcée à une valeur donnée
![]() .
.
(5.5)
L'intérêt de l'agrégation, avec cette notion de fonction de coût
minimal, est de pouvoir manipuler un seul arc
![]() au lieu de tout un SP-graphe
au lieu de tout un SP-graphe
![]() , comme s'il s'agissait d'un arc quelconque avec une fonction de coût
linéaire par morceaux. Nous montrons maintenant que la fonction de coût minimal d'une
SP-relation est toujours convexe si les fonctions de coût sur les arcs non
agrégés sont convexes.
, comme s'il s'agissait d'un arc quelconque avec une fonction de coût
linéaire par morceaux. Nous montrons maintenant que la fonction de coût minimal d'une
SP-relation est toujours convexe si les fonctions de coût sur les arcs non
agrégés sont convexes.
| 5.2.1.1. Agrégation série |
Considérons deux sous-graphes série-parallèles
![]() et
et
![]() , et supposons que leur fonction de coût minimal
, et supposons que leur fonction de coût minimal
![]() et
et
![]() sont connues. Si l'on considère la SP-relation
sont connues. Si l'on considère la SP-relation
![]() (cf. figure 5.7),
(cf. figure 5.7),
![]() et
et
![]() partagent seulement un noeud, la SP-relation n'ajoute donc pas de contrainte de
tension supplémentaire entre eux. Mais si l'on ajoute la contrainte que la tension
principale de
partagent seulement un noeud, la SP-relation n'ajoute donc pas de contrainte de
tension supplémentaire entre eux. Mais si l'on ajoute la contrainte que la tension
principale de
![]() doit être égale à
doit être égale à
![]() , cela impose à
, cela impose à
![]() et
et
![]() , les tensions principales respectivement de
, les tensions principales respectivement de
![]() et
et
![]() , que
, que
![]() . La fonction de coût minimal
. La fonction de coût minimal
![]() de la SP-relation
de la SP-relation
![]() est donc:
est donc:
(5.6)
Cela signifie que
![]() est l'inf-convolution
est l'inf-convolution
![]() . Il est prouvé que cette opération maintient la convexité (e.g.
[Rockafellar70]).
. Il est prouvé que cette opération maintient la convexité (e.g.
[Rockafellar70]).
| 5.2.1.2. Agrégation parallèle |
Considérons deux sous-graphes série-parallèles
![]() et
et
![]() , et supposons que leur fonction de coût minimal
, et supposons que leur fonction de coût minimal
![]() et
et
![]() sont connues. Si l'on considère la SP-relation
sont connues. Si l'on considère la SP-relation
![]() (cf. figure 5.8),
(cf. figure 5.8),
![]() et
et
![]() partagent leur source et leur puits, la seule contrainte de tension entre eux est que
leur tension principale, respectivement
partagent leur source et leur puits, la seule contrainte de tension entre eux est que
leur tension principale, respectivement
![]() et
et
![]() , doivent être égales. Si l'on ajoute la contrainte que la tension
principale de
, doivent être égales. Si l'on ajoute la contrainte que la tension
principale de
![]() doit être égale à
doit être égale à
![]() , cela impose que
, cela impose que
![]() . La fonction de coût minimal
. La fonction de coût minimal
![]() de la SP-relation
de la SP-relation
![]() est donc:
est donc:
(5.7)
Cela signifie que
![]() est simplement la somme
est simplement la somme
![]() , qui est convexe si les fonctions
, qui est convexe si les fonctions
![]() et
et
![]() sont convexes.
sont convexes.
| 5.2.1.3. Fonction de coût minimal t-centrée |
De cette rapide analyse, il est possible d'écrire un algorithme récursif simple
pour construire la fonction de coût minimal
![]() d'un SP-graphe
d'un SP-graphe
![]() . Mais nous sommes plutôt intéressés par déterminer la
tension de coût minimal de
. Mais nous sommes plutôt intéressés par déterminer la
tension de coût minimal de
![]() . Nous proposons maintenant une représentation particulière de la
fonction de coût minimal, de manière à connaître non seulement le
coût de la tension optimale d'une SP-relation, mais également comment construire cette
tension optimale. Pour cela, nous définissons la fonction de coût minimal
. Nous proposons maintenant une représentation particulière de la
fonction de coût minimal, de manière à connaître non seulement le
coût de la tension optimale d'une SP-relation, mais également comment construire cette
tension optimale. Pour cela, nous définissons la fonction de coût minimal
![]() -centrée
-centrée
![]() de
de
![]() comme suit.
comme suit.
(5.8)
Autrement dit
![]() , et la fonction
, et la fonction
![]() représente le coût minimal pour augmenter ou diminuer la tension
principale à partir de la valeur
représente le coût minimal pour augmenter ou diminuer la tension
principale à partir de la valeur
![]() . Centrer la fonction de coût minimal sur la valeur courante
. Centrer la fonction de coût minimal sur la valeur courante
![]() d'un arc agrégé
d'un arc agrégé
![]() permet d'obtenir des informations de coût relatives à la valeur courante
permet d'obtenir des informations de coût relatives à la valeur courante
![]() . Nous choisissons de représenter cette fonction linéaire par morceaux
sous la forme de deux ensembles
. Nous choisissons de représenter cette fonction linéaire par morceaux
sous la forme de deux ensembles
![]() et
et
![]() ,
,
![]() représentant
représentant
![]() sur l'intervalle
sur l'intervalle
![]() et
et
![]() représentant
représentant
![]() sur l'intervalle
sur l'intervalle
![]() . Ces ensembles contiennent simplement la définition de chaque morceau de la
fonction. Un morceau
. Ces ensembles contiennent simplement la définition de chaque morceau de la
fonction. Un morceau
![]() est défini par un triplet de la forme
est défini par un triplet de la forme
![]() , où
, où
![]() représente la pente de la courbe sur le morceau
représente la pente de la courbe sur le morceau
![]() ,
,
![]() la longueur de l'intervalle sur lequel
la longueur de l'intervalle sur lequel
![]() est défini, et
est défini, et
![]() l'ensemble des arcs dont la tension doit être augmentée ou
diminuée pour adapter la tension sur le morceau
l'ensemble des arcs dont la tension doit être augmentée ou
diminuée pour adapter la tension sur le morceau
![]() . Pour des raisons d'efficacité, les morceaux des ensembles
. Pour des raisons d'efficacité, les morceaux des ensembles
![]() et
et
![]() sont triés de la plus petite pente à la plus grande. La figure 5.14
illustre un exemple de fonction de coût minimal
sont triés de la plus petite pente à la plus grande. La figure 5.14
illustre un exemple de fonction de coût minimal
![]() -centrée, définie par les ensembles suivants.
-centrée, définie par les ensembles suivants.
Dans cette figure, considérons la tension principale
![]() de
de
![]() égale à
égale à
![]() . Si l'on souhaite diminuer
. Si l'on souhaite diminuer
![]() d'une unité, il faut diminuer la tension des arcs
d'une unité, il faut diminuer la tension des arcs
![]() et
et
![]() d'une unité, et le coût global de la tension du graphe sera
diminuée de
d'une unité, et le coût global de la tension du graphe sera
diminuée de
![]() unité.
unité.
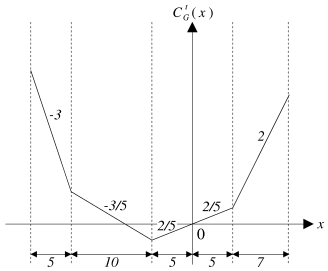 |
| Figure 5.14: Un exemple de fonction de coût minimal t-centrée. |
Notons
![]() la tension de coût minimal d'un graphe
la tension de coût minimal d'un graphe
![]() et
et
![]() . Nous expliquons maintenant comment trouver
. Nous expliquons maintenant comment trouver
![]() et construire la fonction
et construire la fonction
![]() . Remarquons simplement que la fonction de coût minimal
. Remarquons simplement que la fonction de coût minimal
![]() pour un arc non agrégé
pour un arc non agrégé
![]() est représentée par
est représentée par
![]() et
et
![]() avec la tension optimale
avec la tension optimale
![]() . Intéressons-nous maintenant à trouver ces informations pour une
SP-relation.
. Intéressons-nous maintenant à trouver ces informations pour une
SP-relation.
| 5.2.2. Agrégation série |
Considérons le graphe
![]() , et supposons pour les sous-graphes
, et supposons pour les sous-graphes
![]() et
et
![]() que leur tension optimale, respectivement
que leur tension optimale, respectivement
![]() et
et
![]() , et leur fonction de coût minimal, respectivement
, et leur fonction de coût minimal, respectivement
![]() et
et
![]() , sont connues. La tension
, sont connues. La tension
![]() formée des deux tensions
formée des deux tensions
![]() et
et
![]() est optimale, puisque la relation série
est optimale, puisque la relation série
![]() n'entraîne aucune contrainte supplémentaire entre
n'entraîne aucune contrainte supplémentaire entre
![]() et
et
![]() .
.
Pour augmenter la tension principale
![]() du graphe
du graphe
![]() , nous pouvons choisir d'augmenter celle du sous-graphe
, nous pouvons choisir d'augmenter celle du sous-graphe
![]() , i.e.
, i.e.
![]() , ou celle de
, ou celle de
![]() , i.e.
, i.e.
![]() . Observons
. Observons
![]() et
et
![]() les premiers morceaux respectivement de
les premiers morceaux respectivement de
![]() et de
et de
![]() . Afin d'effectuer une augmentation optimale, il faut choisir d'augmenter
. Afin d'effectuer une augmentation optimale, il faut choisir d'augmenter
![]() si
si
![]() , ou
, ou
![]() sinon. Supposons que
sinon. Supposons que
![]() ait été augmentée, cette opération ne peut pas
dépasser
ait été augmentée, cette opération ne peut pas
dépasser
![]() unités. Ensuite il est nécessaire d'appliquer à nouveau le
même raisonnement sur les nouvelles valeurs de
unités. Ensuite il est nécessaire d'appliquer à nouveau le
même raisonnement sur les nouvelles valeurs de
![]() et
et
![]() . Cette analyse peut être faite également pour la diminution de
. Cette analyse peut être faite également pour la diminution de
![]() .
.
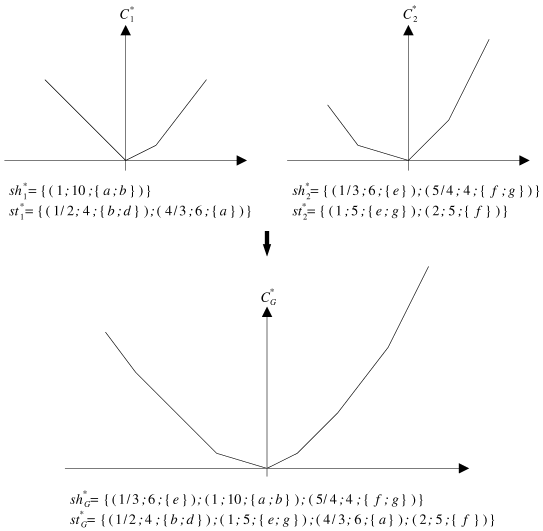 |
| Figure 5.15: Un exemple de construction de la fonction de coût minimal d'une relation série. |
En conclusion, la fonction
![]() est représentée par les ensembles
est représentée par les ensembles
![]() et
et
![]() triés de la plus petite pente à la plus grande. La figure 5.15 montre un
exemple de construction de la fonction de coût minimal
triés de la plus petite pente à la plus grande. La figure 5.15 montre un
exemple de construction de la fonction de coût minimal
![]() -centrée d'une relation série, la procédure étant
résumée par l'algorithme 5.6.
-centrée d'une relation série, la procédure étant
résumée par l'algorithme 5.6.
Algorithme 5.6: agrégerSérie(fonction
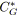 ,fonction
,fonction
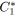 ,fonction
,fonction
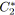 )
)
tant que
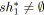 et
et
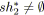 faire
faire
soit
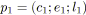 premier morceau de
premier morceau de
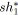 ;
;
soit
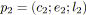 premier morceau de
premier morceau de
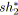 ;
;
si
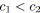 alors
alors
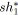

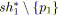 ;
; 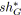

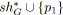 ;
;
sinon
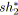

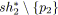 ;
; 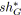

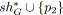 ;
;
fin tant que;
tant que
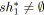 faire
faire
soit
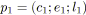 premier morceau de
premier morceau de
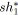 ;
;
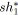

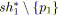 ;
; 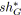

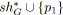 ;
;
fin tant que;
tant que
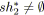 faire
faire
soit
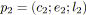 premier morceau de
premier morceau de
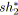 ;
;
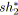

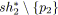 ;
; 

 ;
;
fin tant que;
/* Procédure similaire pour
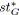 . */
. */
...
fin algorithme; Notons
![]() et
et
![]() les nombres de morceaux de
les nombres de morceaux de
![]() et
et
![]() ,
,
![]() possède donc
possède donc
![]() morceaux, et la procédure de construction de la fonction de coût minimal
et de la tension optimale d'une relation série nécessite
morceaux, et la procédure de construction de la fonction de coût minimal
et de la tension optimale d'une relation série nécessite
![]() opérations:
opérations:
![]() opérations pour parcourir les
opérations pour parcourir les
![]() morceaux des fonctions de coût minimal, et
morceaux des fonctions de coût minimal, et
![]() opérations pour copier un ensemble d'au plus
opérations pour copier un ensemble d'au plus
![]() arcs pour chaque morceau.
arcs pour chaque morceau.
| 5.2.3. Agrégation parallèle |
Considérons maintenant le graphe
![]() , et supposons pour les sous-graphes
, et supposons pour les sous-graphes
![]() et
et
![]() que leur tension optimale, respectivement
que leur tension optimale, respectivement
![]() et
et
![]() , et leur fonction de coût minimal, respectivement
, et leur fonction de coût minimal, respectivement
![]() et
et
![]() sont connues. La relation parallèle est possible seulement si
sont connues. La relation parallèle est possible seulement si
![]() , la tension du graphe
, la tension du graphe
![]() ne sera valide qu'à cette condition. Comme nous devons trouver la tension
optimale
ne sera valide qu'à cette condition. Comme nous devons trouver la tension
optimale
![]() du graphe
du graphe
![]() , une méthode est nécessaire pour égaliser
, une méthode est nécessaire pour égaliser
![]() et
et
![]() de manière optimale, i.e. rendre la tension
de manière optimale, i.e. rendre la tension
![]() formée de
formée de
![]() et
et
![]() optimale.
optimale.
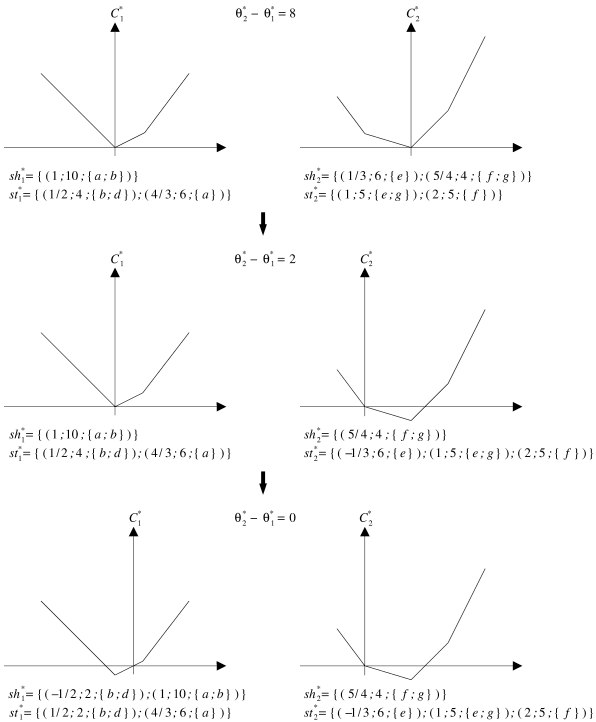 |
| Figure 5.16: Un exemple d'égalisation des tensions lors d'une sérialisation. |
Supposons que
![]() , pour égaliser
, pour égaliser
![]() et
et
![]() , il faut augmenter
, il faut augmenter
![]() et/ou diminuer
et/ou diminuer
![]() . Observons donc
. Observons donc
![]() et
et
![]() , les premiers morceaux respectivement de
, les premiers morceaux respectivement de
![]() et
et
![]() . Afin d'effectuer un rapprochement des deux tensions de manière optimale, il
faut choisir d'augmenter
. Afin d'effectuer un rapprochement des deux tensions de manière optimale, il
faut choisir d'augmenter
![]() si
si
![]() , ou de diminuer
, ou de diminuer
![]() sinon. Supposons que
sinon. Supposons que
![]() ait été diminuée, cette opération ne peut dépasser
ait été diminuée, cette opération ne peut dépasser
![]() unités. Ensuite il est nécessaire d'appliquer le même raisonnement
sur les nouvelles valeurs de
unités. Ensuite il est nécessaire d'appliquer le même raisonnement
sur les nouvelles valeurs de
![]() et
et
![]() . Cette opération est répétée jusqu'à ce que
. Cette opération est répétée jusqu'à ce que
![]() .
.
Algorithme 5.7: égaliserTensionsParallèles( fonction,
fonction,
tension,tension
)
tant quefaire
siet
alors arrêter; /* Tension non réalisable. */
soitle premier morceau de
si
;
soitle premier morceau de
si
;
siou
alors /* Augmentation tension. */


;
pour toutfaire
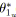

;
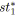

;
sialors
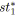

;
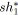

;
sinon /* Diminution tension. */


;
pour toutfaire
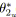

;
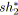

;
sialors
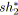

;
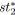

;
fin si;
fin tant que;
/* Procédure similaire pour le cas. */
...
fin algorithme;
La figure 5.16 illustre un exemple d'égalisation de tensions principales entre deux
sous-graphes associés par une relation parallèle. L'algorithme 5.7 résume
cette procédure. Une fois les deux tensions principales égales, il est alors possible
de construire
![]() centrée sur
centrée sur
![]() , comme le montre l'algorithme 5.8. La figure 5.17 illustre cette procédure par
un exemple.
, comme le montre l'algorithme 5.8. La figure 5.17 illustre cette procédure par
un exemple.
Algorithme 5.8: agrégerParallèle(fonction
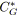 ,fonction
,fonction
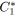 ,fonction
,fonction
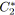 )
)
tant que
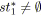 et
et
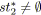 faire
faire
soit
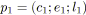 le premier morceau de
le premier morceau de
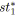 ;
;
soit
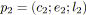 le premier morceau de
le premier morceau de
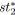 ;
;


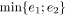 ;
;
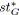

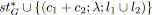 ;
;
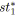

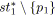 ;
;
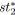

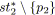 ;
;
si
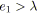 alors
alors
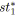

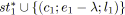 ;
;
si
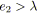 alors
alors
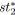

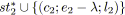 ;
;
fin tant que;
/* Procédure similaire pour
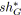 . */
. */
...
fin algorithme; Notons
![]() et
et
![]() les nombres de morceaux de
les nombres de morceaux de
![]() et
et
![]() . Il est possible de vérifier que l'exécution de l'algorithme 5.7 suivi
de 5.8 construit
. Il est possible de vérifier que l'exécution de l'algorithme 5.7 suivi
de 5.8 construit
![]() avec au plus
avec au plus
![]() morceaux (le premier algorithme crée au plus un morceau supplémentaire,
et de la figure 5.17, il est évident que le second algorithme crée au plus
morceaux (le premier algorithme crée au plus un morceau supplémentaire,
et de la figure 5.17, il est évident que le second algorithme crée au plus
![]() morceaux). La procédure complète de construction de la fonction de
coût minimal et de la tension optimale d'une relation parallèle nécessite alors
morceaux). La procédure complète de construction de la fonction de
coût minimal et de la tension optimale d'une relation parallèle nécessite alors
![]() opérations: la procédure d'égalisation des tensions parcours au
plus
opérations: la procédure d'égalisation des tensions parcours au
plus
![]() morceaux des fonctions de coût minimal, et copie au plus
morceaux des fonctions de coût minimal, et copie au plus
![]() arcs pour chaque morceau; de même l'algorithme 5.8 crée au plus
arcs pour chaque morceau; de même l'algorithme 5.8 crée au plus
![]() morceaux et copie pour chacun au plus
morceaux et copie pour chacun au plus
![]() arcs.
arcs.
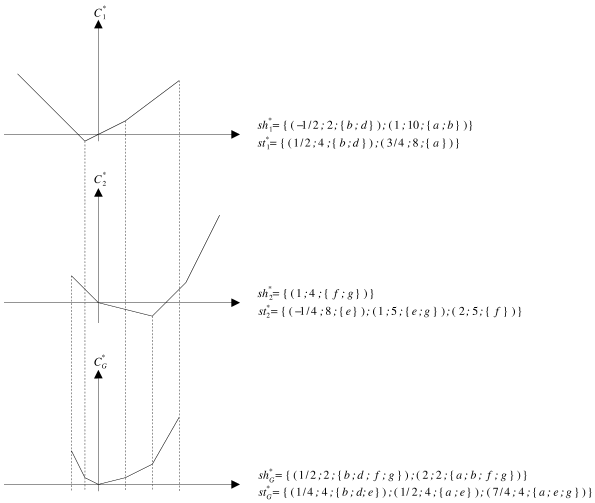 |
| Figure 5.17: Un exemple de construction de la fonction de coût minimal d'une relation parallèle. |
| 5.2.4. Tension optimale |
A partir des algorithmes présentés précédemment, il est possible de
proposer une méthode permettant de déterminer la tension optimale
![]() et la fonction de coût minimal
et la fonction de coût minimal
![]() d'un SP-graphe
d'un SP-graphe
![]() entier. Cet algorithme repose sur le SP-arbre
entier. Cet algorithme repose sur le SP-arbre
![]() associé à
associé à
![]() : partant de ses feuilles, il suffit d'appliquer récursivement les
méthodes d'agrégation sur des SP-relations détaillées aux sections
précédentes (cf. algorithme 5.9). Nous montrons maintenant que cette procédure
est polynômiale.
: partant de ses feuilles, il suffit d'appliquer récursivement les
méthodes d'agrégation sur des SP-relations détaillées aux sections
précédentes (cf. algorithme 5.9). Nous montrons maintenant que cette procédure
est polynômiale.
La méthode d'agrégation nécessite opérations.
(5.9)
Preuve:
Nous avons établi que chaque agrégation effectue
![]() opérations. En début de chapitre, il a été signalé
qu'un SP-graphe possède
opérations. En début de chapitre, il a été signalé
qu'un SP-graphe possède
![]() SP-relations. La méthode d'agrégation nécessite donc
SP-relations. La méthode d'agrégation nécessite donc
![]() opérations. Nous avons également expliqué que, pour chaque
SP-relation, si
opérations. Nous avons également expliqué que, pour chaque
SP-relation, si
![]() et
et
![]() sont les nombres de morceaux de
sont les nombres de morceaux de
![]() et
et
![]() , alors
, alors
![]() possède au plus
possède au plus
![]() morceaux. Autrement dit, si chaque arc non agrégé possède deux
morceaux dans sa fonction de coût, alors la fonction de coût minimal du SP-graphe
complet ne peut pas excéder
morceaux. Autrement dit, si chaque arc non agrégé possède deux
morceaux dans sa fonction de coût, alors la fonction de coût minimal du SP-graphe
complet ne peut pas excéder
![]() morceaux. La méthode d'agrégation nécessite donc bien
morceaux. La méthode d'agrégation nécessite donc bien
![]() opérations.
opérations.
![]()
Algorithme 5.9: agréger(arbre
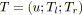 ,tension
,tension
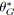 ,fonction
,fonction
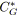 )
)
si
 alors
alors
agréger(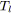 ,
,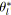 ,
, );
);
agréger(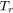 ,
,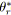 ,
,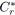 );
);
si
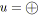 alors
alors
agrégerSérie(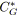 ,
, ,
,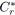 );
);
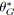

 ;
;
sinon si
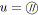 alors
alors
égaliserTensionsParallèles( ,
,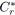 ,
,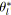 ,
,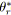 );
);
agrégerParallèle(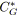 ,
, ,
,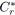 );
);
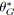

 ;
;
sinon
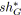

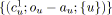 ;
;
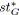

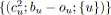 ;
;
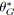

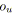 ;
;
fin si;
fin si;
fin algorithme;| 5.2.5. Conclusion |
Nous proposons ici de comparer l'efficacité pratique des méthodes de résolution du problème de tension de coût minimal présentées au chapitre précédent et de la méthode d'agrégation sur des graphes série-parallèles par rapport à des graphes quelconques. Pour connaître en détails comment ont été dirigés ces essais (méthode de génération des problèmes, compilateur utilisé...), le lecteur peut consulter l'annexe. Nous précisons seulement que l'outil CPLEX 6.0 a été utilisé avec ses paramètres par défaut pour résoudre les programmes linéaires et que les problèmes générés ont des bornes de tension et des coûts entiers. Les temps de calcul sont exprimés en secondes sur une machine RISC-6000 à 160 MHz.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Tableau 5.1: Comparatif des résultats numériques des algorithmes
de tension de coût minimal sur des SP-graphes par rapport à des graphes quelconques. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Le tableau 5.1 présente le temps de résolution (avec
![]() ) de la programmation linéaire (modèle
) de la programmation linéaire (modèle
![]() ), de la mise à conformité (algorithme 4.4) et de la mise à
l'échelle du dual (algorithme 4.13). Les deux premières méthodes se comportent
nettement mieux, même si la mise à conformité profite un peu plus de la
simplification du problème. En revanche, la mise à l'échelle du dual est plus
décevante. Il semblerait que la structure série-parallèle des graphes
complique l'équilibrage des noeuds (cf. section 4.6). Même avec la technique
d'implémentation par vague (wave implementation [Ahuja93]), qui améliore la complexité de la méthode,
nous n'avons pas abouti à de meilleures performances.
), de la mise à conformité (algorithme 4.4) et de la mise à
l'échelle du dual (algorithme 4.13). Les deux premières méthodes se comportent
nettement mieux, même si la mise à conformité profite un peu plus de la
simplification du problème. En revanche, la mise à l'échelle du dual est plus
décevante. Il semblerait que la structure série-parallèle des graphes
complique l'équilibrage des noeuds (cf. section 4.6). Même avec la technique
d'implémentation par vague (wave implementation [Ahuja93]), qui améliore la complexité de la méthode,
nous n'avons pas abouti à de meilleures performances.
Comme nous pouvions l'espérer, la méthode d'agrégation fournit des temps
de calcul significativement meilleurs que les autres méthodes. En outre, elle semble
beaucoup moins sensible à la taille du graphe: la mise à conformité et la mise
à l'échelle offrent un rapport entre
![]() et
et
![]() entre le temps de calcul des plus petites instances et des plus grandes;
l'agrégation propose elle un rapport d'environ
entre le temps de calcul des plus petites instances et des plus grandes;
l'agrégation propose elle un rapport d'environ
![]() ; seule la programmation linéaire se rapproche de ce comportement avec un
rapport de
; seule la programmation linéaire se rapproche de ce comportement avec un
rapport de
![]() . L'efficacité de la méthode d'agrégation pour des graphes
série-parallèles est telle qu'il serait intéressant de l'exploiter pour
résoudre le problème de la tension de coût minimal sur des graphes
"presque" série-parallèles, plus proches des cas réels de
synchronisation hypermédia.
. L'efficacité de la méthode d'agrégation pour des graphes
série-parallèles est telle qu'il serait intéressant de l'exploiter pour
résoudre le problème de la tension de coût minimal sur des graphes
"presque" série-parallèles, plus proches des cas réels de
synchronisation hypermédia.
| 5.3. GRAPHES PRESQUE SERIE-PARALLELES |
Notamment à cause de la relation overlaps (cf. figure 5.9), les graphes temporels issus de synchronisations hypermédia ne sont pas série-parallèles, mais restent en pratique très proches de cette structure particulière. Nous introduisons ici la notion de graphe presque série-parallèle pour caractériser des graphes dont la structure de base est série-parallèle mais est perturbée par l'ajout de quelques arcs. Cette dernière section propose une méthode pour résoudre le problème de la tension de coût minimal sur ce type de graphe, l'objectif étant d'exploiter la méthode d'agrégation pour fournir une méthode plus efficace que les méthodes de mise à conformité et de mise à l'échelle du dual pour des graphes presque série-parallèles. Cependant les résultats numériques montrent que cette méthode est très inefficace sur des graphes quelconques.
L'idée de la méthode de résolution consiste à décomposer un graphe temporel en sous-graphes série-parallèles, ses composantes série-parallèles. L'optimisation de la tension sur ces sous-graphes est effectuée par la méthode d'agrégation. Ainsi, chaque composante est agrégée et représentée par un seul arc avec un coût linéaire par morceaux. Ensuite, dans un ordre précis, les composantes sont rassemblées une à une, pour progressivement reformer le graphe original. Lors de cette phase de reconstruction, la mise à conformité est employée pour conserver une tension optimale. Dans un premier temps, nous précisons la notion de composantes série-parallèles. Nous décrivons ensuite la phase de reconstruction et présentons quelques résultats numériques, en supposant la décomposition déjà effectuée (elle est obtenue lors de la génération des jeux d'essais). Enfin, nous présentons et comparons deux méthodes simples de décomposition d'un graphe quelconque en composantes série-parallèles.
| 5.3.1. Composantes série-parallèles |
Un sous-graphe série-parallèle d'un graphe
![]() est appelé composante série-parallèle, ou
SP-composante, de
est appelé composante série-parallèle, ou
SP-composante, de
![]() . Une SP-composante est dite maximale si elle n'est pas contenue strictement
dans une autre. Une partition
. Une SP-composante est dite maximale si elle n'est pas contenue strictement
dans une autre. Une partition
![]() des arcs de
des arcs de
![]() définit une décomposition série-parallèle, ou
SP-décomposition, du graphe
définit une décomposition série-parallèle, ou
SP-décomposition, du graphe
![]() où chaque ensemble d'arcs de
où chaque ensemble d'arcs de
![]() induit un sous-graphe série-parallèle de
induit un sous-graphe série-parallèle de
![]() . Une SP-décomposition du graphe
. Une SP-décomposition du graphe
![]() est donc un ensemble de SP-composantes deux à deux disjointes, en termes
d'arcs, et dont l'union est égale à
est donc un ensemble de SP-composantes deux à deux disjointes, en termes
d'arcs, et dont l'union est égale à
![]() .
.
Pour les besoins de l'algorithme de reconstruction, nous supposons un ordre partiel sur les
composantes d'une SP-décomposition, telle que si la source ou le puits d'une composante
![]() appartiennent à la composante
appartiennent à la composante
![]() , alors
, alors
![]() . Nous montrons dans la section sur les méthodes de décomposition qu'il
existe toujours une décomposition avec un tel ordre pour n'importe quel graphe.
. Nous montrons dans la section sur les méthodes de décomposition qu'il
existe toujours une décomposition avec un tel ordre pour n'importe quel graphe.
Un graphe presque série-parallèle
![]() est un graphe formé de l'union d'un SP-graphe
est un graphe formé de l'union d'un SP-graphe
![]() et d'un ensemble d'arcs
et d'un ensemble d'arcs
![]() , i.e.
, i.e.
![]() ,
,
![]() étant l'une des plus grandes SP-composantes maximales de
étant l'une des plus grandes SP-composantes maximales de
![]() . Le rapport
. Le rapport
![]() est appelé la SP-perturbation du graphe
est appelé la SP-perturbation du graphe
![]() . D'après cette définition, tout graphe est presque
série-parallèle, avec une SP-perturbation plus ou moins élevée, mais le
terme presque série-parallèle est naturellement réservé aux
graphes avec une SP-perturbation faible, le seuil restant à définir. Nous proposons
maintenant une méthode d'optimisation pour des graphes avec une SP-perturbation faible, de
l'ordre de quelques pourcents. Des résultats numériques montrent la SP-perturbation
maximale pour laquelle la nouvelle approche est efficace, ce qui sera le seuil au delà
duquel les graphes ne seront plus considérés presque série-parallèles
par la suite. Notons que la SP-perturbation d'un graphe ne peut être mesurée que si
l'une de ses plus grandes SP-composantes maximales est connue, problème qui reste ouvert et
que nous aborderons plus tard.
. D'après cette définition, tout graphe est presque
série-parallèle, avec une SP-perturbation plus ou moins élevée, mais le
terme presque série-parallèle est naturellement réservé aux
graphes avec une SP-perturbation faible, le seuil restant à définir. Nous proposons
maintenant une méthode d'optimisation pour des graphes avec une SP-perturbation faible, de
l'ordre de quelques pourcents. Des résultats numériques montrent la SP-perturbation
maximale pour laquelle la nouvelle approche est efficace, ce qui sera le seuil au delà
duquel les graphes ne seront plus considérés presque série-parallèles
par la suite. Notons que la SP-perturbation d'un graphe ne peut être mesurée que si
l'une de ses plus grandes SP-composantes maximales est connue, problème qui reste ouvert et
que nous aborderons plus tard.
| 5.3.2. Méthode de reconstruction |
Supposons
![]() une SP-décomposition d'un graphe
une SP-décomposition d'un graphe
![]() triée selon l'ordre décrit à la section précédente.
La procédure itérative de reconstruction du graphe
triée selon l'ordre décrit à la section précédente.
La procédure itérative de reconstruction du graphe
![]() à sa tension optimale à partir de sa SP-décomposition est la
suivante. La figure 5.18 illustre ce processus.
à sa tension optimale à partir de sa SP-décomposition est la
suivante. La figure 5.18 illustre ce processus.
- Etape 1: Agrégation.
Supposons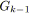 le graphe obtenu à l'itération
le graphe obtenu à l'itération
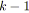 (au départ,
(au départ,
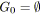 ). Pour construire
). Pour construire
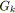 , on considère
, on considère
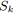 la
la
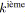 composante de l'ensemble trié
composante de l'ensemble trié
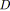 . La tension optimale
. La tension optimale
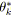 et la fonction de coût minimal
et la fonction de coût minimal
 de
de
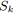 sont obtenues par la méthode d'agrégation (cf. algorithme 5.9). On tente
ensuite d'ajouter l'arc agrégé
sont obtenues par la méthode d'agrégation (cf. algorithme 5.9). On tente
ensuite d'ajouter l'arc agrégé
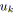 représentant
représentant
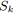 au graphe
au graphe
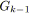 . Si l'origine et la destination de cet arc sont des noeuds du graphe
. Si l'origine et la destination de cet arc sont des noeuds du graphe
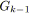 , alors l'arc peut être ajouté directement (cf. étape 3). En
revanche, si une extrémité de l'arc n'existe pas, il faut désagréger
l'arc dont la composante qu'il représente contient l'extrémité manquante (cf.
étape 2). Cet arc existe forcément grâce à l'ordre partiel des
composantes dans la SP-décomposition. Dans l'exemple de la figure 5.18, lorsque l'arc
agrégé représentant la composante
, alors l'arc peut être ajouté directement (cf. étape 3). En
revanche, si une extrémité de l'arc n'existe pas, il faut désagréger
l'arc dont la composante qu'il représente contient l'extrémité manquante (cf.
étape 2). Cet arc existe forcément grâce à l'ordre partiel des
composantes dans la SP-décomposition. Dans l'exemple de la figure 5.18, lorsque l'arc
agrégé représentant la composante
 est ajouté, les noeuds
est ajouté, les noeuds
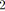 et
et
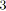 ne sont pas présents dans
ne sont pas présents dans
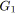 , il faut donc désagréger l'arc
, il faut donc désagréger l'arc
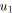 qui représente la composante
qui représente la composante
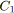 et qui contient ces deux noeuds. Il faut remarquer que dans une
SP-décomposition où l'on a obtenu la plus grande composante possible, celle-ci sera
souvent ajoutée la première et désagrégée dès la seconde
itération.
et qui contient ces deux noeuds. Il faut remarquer que dans une
SP-décomposition où l'on a obtenu la plus grande composante possible, celle-ci sera
souvent ajoutée la première et désagrégée dès la seconde
itération.
- Etape 2: Désagrégation.
Désagréger un arc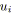 consiste à le remplacer par la SP-composante
consiste à le remplacer par la SP-composante
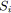 qu'il représente. Cependant, le bon fonctionnement de la procédure de
reconstruction repose sur la propriété qu'à chaque itération
qu'il représente. Cependant, le bon fonctionnement de la procédure de
reconstruction repose sur la propriété qu'à chaque itération
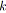 , les arcs du graphe
, les arcs du graphe
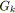 , agrégés ou non, sont conformes. L'arc
, agrégés ou non, sont conformes. L'arc
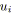 est donc conforme, en se basant sur la fonction de coût
est donc conforme, en se basant sur la fonction de coût
 . A partir de la tension
. A partir de la tension
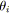 et du flot
et du flot
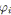 de l'arc agrégé
de l'arc agrégé
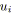 , il faut déterminer la tension et le flot équivalent sur la composante
, il faut déterminer la tension et le flot équivalent sur la composante
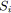 , i.e. la tension principale de
, i.e. la tension principale de
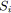 doit être
doit être
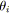 , le flot principal (i.e. entre la source et le puits) de
, le flot principal (i.e. entre la source et le puits) de
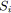 doit être
doit être
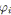 , et le coût total de
, et le coût total de
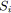 doit être le même que celui de
doit être le même que celui de
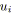 . La tension est déterminée à partir de la fonction de coût
minimal
. La tension est déterminée à partir de la fonction de coût
minimal
 , et un algorithme de recherche de flot compatible (cf. la sous-section suivante pour
les détails) permet de déterminer un flot tel que tous les arcs sont conformes.
, et un algorithme de recherche de flot compatible (cf. la sous-section suivante pour
les détails) permet de déterminer un flot tel que tous les arcs sont conformes.
- Etape 3: Reconstruction.
L'arc agrégé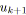 peut alors être ajouté au graphe
peut alors être ajouté au graphe
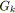 pour former le graphe
pour former le graphe
 . La tension de cet arc est établie à partir du potentiel de ses noeuds,
et son flot est fixé à
. La tension de cet arc est établie à partir du potentiel de ses noeuds,
et son flot est fixé à
 . De cette manière, la tension et le flot sur tout le graphe sont valides. En
outre, tous les arcs sont conformes excepté celui qui vient d'être ajouté. Il
faut donc le rendre conforme en appliquant par exemple la procédure d'amélioration
d'un arc vue au chapitre 4. La seule différence réside dans le fait que les
coûts traités ont plus de deux morceaux: les arcs désagrégés
possèdent bien un coût avec deux morceaux, mais les arcs agrégés ont
comme coût leur fonction de coût minimal. Cette différence ne modifie pas la
complexité de la procédure (le nombre total de morceaux ne dépassant pas au
pire
. De cette manière, la tension et le flot sur tout le graphe sont valides. En
outre, tous les arcs sont conformes excepté celui qui vient d'être ajouté. Il
faut donc le rendre conforme en appliquant par exemple la procédure d'amélioration
d'un arc vue au chapitre 4. La seule différence réside dans le fait que les
coûts traités ont plus de deux morceaux: les arcs désagrégés
possèdent bien un coût avec deux morceaux, mais les arcs agrégés ont
comme coût leur fonction de coût minimal. Cette différence ne modifie pas la
complexité de la procédure (le nombre total de morceaux ne dépassant pas au
pire
 dans tout le graphe), mais en pratique elle induit, comme le montrent les
résultats numériques, un ralentissement d'un facteur constant (e.g. tableau 5.2).
dans tout le graphe), mais en pratique elle induit, comme le montrent les
résultats numériques, un ralentissement d'un facteur constant (e.g. tableau 5.2).
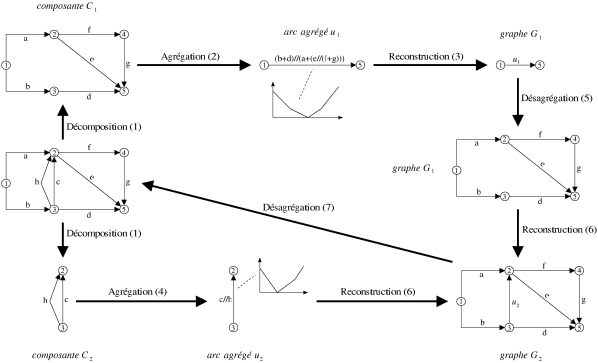 |
| Figure 5.18: Un exemple de reconstruction. |
Cette procédure est répétée jusqu'à ce que toutes les composantes soient ajoutées au graphe. A la dernière itération, au moins un arc, le dernier ajouté, est agrégé. Il faut donc terminer la reconstruction par la désagrégation des arcs qui ne l'ont pas été au cours de la procédure (cf. étape 2). Le graphe ainsi obtenu est bien l'original avec tous ses arcs conformes. L'enchaînement des étapes de cette reconstruction est résumé succinctement dans l'algorithme 5.10.
Algorithme 5.10: reconstruire(ensemble
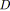 ,tension
,tension
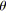 )
)
soit
 potentiel associé à
potentiel associé à
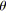 ;
;
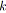

 ;
;
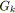

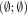 ;
;
tant que
 faire
faire
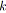

 ;
;
soit
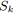 la
la
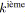 composante de
composante de
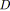 ;
;
soit
 et
et
 la source et le puits de
la source et le puits de
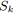 ;
;
soit
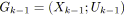 ;
;
... /* Etape 1: Agréger
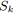 en l'arc
en l'arc
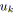 . */
. */
si
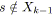 alors
alors
soit
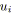 l'arc agrégé de
l'arc agrégé de
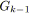 contenant
contenant
 ;
;
... /* Etape 2: Désagréger
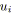 . */
. */
fin si;
si
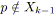 alors
alors
soit
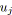 l'arc agrégé de
l'arc agrégé de
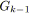 contenant
contenant
 ;
;
... /* Etape 2: Désagréger
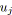 . */
. */
fin si;
/* Etape 3: Reconstruction. */
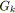

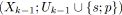 ;
;
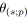

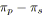 ;
;
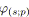

 ;
;
tant que
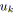 non conforme faire améliorerConformité(
non conforme faire améliorerConformité(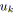 ,
,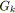 ,
,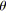 ,
,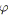 );
);
fin tant que;
fin algorithme;| 5.3.2.1. Algorithme de construction d'un flot conforme |
Au cours de la phase de reconstruction, nous avons vu qu'il était nécessaire,
pour une composante série-parallèle
![]() dont on connaît le flot principal
dont on connaît le flot principal
![]() (i.e. le flot entre sa source et son puits) et la tension optimale
(i.e. le flot entre sa source et son puits) et la tension optimale
![]() (par rapport à tout le graphe
(par rapport à tout le graphe
![]() ), de déterminer un flot sur tous les arcs de la composante de manière
à ce qu'ils soient conformes (cf. étape 2). Il est possible en regardant la courbe de
conformité d'un arc
), de déterminer un flot sur tous les arcs de la composante de manière
à ce qu'ils soient conformes (cf. étape 2). Il est possible en regardant la courbe de
conformité d'un arc
![]() de déterminer, par rapport à la tension
de déterminer, par rapport à la tension
![]() de l'arc, l'intervalle dans lequel son flot
de l'arc, l'intervalle dans lequel son flot
![]() doit se trouver pour que l'arc soit conforme (cf. figure 5.19). De cette
manière, à chaque arc
doit se trouver pour que l'arc soit conforme (cf. figure 5.19). De cette
manière, à chaque arc
![]() est associé un intervalle de flot
est associé un intervalle de flot
![]() .
.
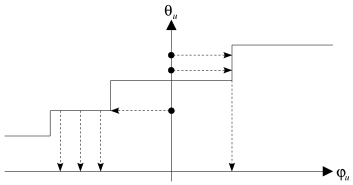 |
| Figure 5.19: Construction d'un flot conforme, connaissant la tension optimale. |
En ajoutant un arc
![]() de capacité de flot
de capacité de flot
![]() entre le puits et la source de la composante série-parallèle
entre le puits et la source de la composante série-parallèle
![]() , trouver un flot qui rend tous les arcs conformes sur la composante
, trouver un flot qui rend tous les arcs conformes sur la composante
![]() revient à déterminer un flot compatible avec les intervalles
établis sur la composante
revient à déterminer un flot compatible avec les intervalles
établis sur la composante
![]() complétée de l'arc
complétée de l'arc
![]() . Une condition nécessaire et suffisante pour qu'un tel flot existe est, pour
tout cocycle
. Une condition nécessaire et suffisante pour qu'un tel flot existe est, pour
tout cocycle
![]() ,
,
![]() (cf. [Gondran79]). Cette condition est toujours
vérifiée, car
(cf. [Gondran79]). Cette condition est toujours
vérifiée, car
![]() représente le coût unitaire d'augmentation de la tension de
représente le coût unitaire d'augmentation de la tension de
![]() et
et
![]() le coût unitaire de diminution de la tension de
le coût unitaire de diminution de la tension de
![]() , un cocycle avec une telle somme négative signifierait qu'une diminution du
coût global de la tension est possible.
, un cocycle avec une telle somme négative signifierait qu'une diminution du
coût global de la tension est possible.
L'une des meilleures complexités pour résoudre le problème du flot
compatible est
![]() (cf. [Ahuja93]), mais nous avons choisi d'utiliser une
méthode similaire à l'agrégation, i.e. basée sur une approche
récursive exploitant le SP-arbre associé à la composante, car elle est
très simple à implémenter et polynômiale. Cette méthode
récursive tente de déterminer le flot principal
(cf. [Ahuja93]), mais nous avons choisi d'utiliser une
méthode similaire à l'agrégation, i.e. basée sur une approche
récursive exploitant le SP-arbre associé à la composante, car elle est
très simple à implémenter et polynômiale. Cette méthode
récursive tente de déterminer le flot principal
![]() (i.e. entre la source et le puits) minimal d'un SP-graphe
(i.e. entre la source et le puits) minimal d'un SP-graphe
![]() , en récoltant en même temps des informations permettant d'augmenter le
flot
, en récoltant en même temps des informations permettant d'augmenter le
flot
![]() efficacement par la suite. De manière similaire à l'agrégation,
ces informations sont récoltées sous la forme d'un ensemble
efficacement par la suite. De manière similaire à l'agrégation,
ces informations sont récoltées sous la forme d'un ensemble
![]() constitué de couples
constitué de couples
![]() signifiant que l'on peut augmenter le flot des arcs de l'ensemble
signifiant que l'on peut augmenter le flot des arcs de l'ensemble
![]() au maximum de
au maximum de
![]() , le flot sur le graphe restant compatible. Ainsi, pour la composante
, le flot sur le graphe restant compatible. Ainsi, pour la composante
![]() , on obtiendra le flot principal minimal et comment l'augmenter efficacement à
la valeur
, on obtiendra le flot principal minimal et comment l'augmenter efficacement à
la valeur
![]() .
.
Algorithme 5.11: égaliserFlotsSéries(fonction,fonction
,
flot,flot
)
tant quefaire
sialors arrêter; /* Flot non réalisable. */
soit;


;
pour toutfaire


;
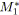

;
sialors
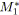

;
fin tant que;
/* Procédure similaire pour le cas. */
...
fin algorithme;
Considérons le graphe
![]() , et supposons pour les sous-graphes
, et supposons pour les sous-graphes
![]() et
et
![]() que leur flot minimal, respectivement
que leur flot minimal, respectivement
![]() et
et
![]() , et leur ensemble, respectivement
, et leur ensemble, respectivement
![]() et
et
![]() , sont connus. La relation série est possible seulement si
, sont connus. La relation série est possible seulement si
![]() , le flot du graphe
, le flot du graphe
![]() n'est valide qu'à cette condition. Il faut une procédure
d'égalisation de deux flots en série, le flot principal résultant étant
minimal. A partir des ensembles
n'est valide qu'à cette condition. Il faut une procédure
d'égalisation de deux flots en série, le flot principal résultant étant
minimal. A partir des ensembles
![]() et
et
![]() , il est possible de proposer une approche polynômiale, similaire à la
méthode d'égalisation de tensions parallèles (cf. algorithme 5.11).
, il est possible de proposer une approche polynômiale, similaire à la
méthode d'égalisation de tensions parallèles (cf. algorithme 5.11).
Algorithme 5.12: minimiserSérie(fonction,fonction
,
fonction)
tant queet
faire
soit;
soit;


;
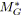

;
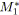

;
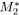

;
sialors
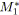

;
sialors
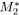

;
fin tant que;
fin algorithme;
Une fois les deux flots principaux
![]() et
et
![]() égaux, il faut construire l'ensemble
égaux, il faut construire l'ensemble
![]() de la relation série
de la relation série
![]() . L'approche est similaire à la méthode d'agrégation de deux
sous-graphes parallèles (cf. algorithme 5.12).
. L'approche est similaire à la méthode d'agrégation de deux
sous-graphes parallèles (cf. algorithme 5.12).
Considérons maintenant le graphe
![]() , et supposons pour les sous-graphes
, et supposons pour les sous-graphes
![]() et
et
![]() que leur flot minimal, respectivement
que leur flot minimal, respectivement
![]() et
et
![]() , et leur ensemble, respectivement
, et leur ensemble, respectivement
![]() et
et
![]() , sont connus. Le flot principal minimal
, sont connus. Le flot principal minimal
![]() est égal à
est égal à
![]() , et l'ensemble
, et l'ensemble
![]() est l'union
est l'union
![]() . La procédure complète pour déterminer le flot minimal d'un
graphe
. La procédure complète pour déterminer le flot minimal d'un
graphe
![]() est détaillée dans l'algorithme 5.13.
est détaillée dans l'algorithme 5.13.
Algorithme 5.13: minimiserFlot(arbre
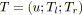 ,flot
,flot
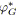 ,fonction
,fonction
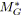 )
)
si
 alors
alors
minimiserFlot(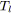 ,
,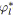 ,
,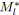 );
);
minimiserFlot(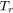 ,
,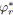 ,
, );
);
si
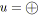 alors
alors
égaliserFlotsSéries(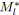 ,
, ,
,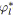 ,
,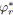 );
);
minimiserSérie(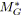 ,
,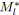 ,
, );
);
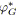

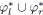 ;
;
sinon si
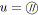 alors
alors
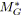

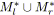 ;
;
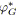

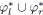 ;
;
sinon
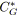

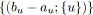 ;
;
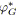

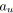 ;
;
fin si;
fin si;
fin algorithme; Une fois le flot minimal
![]() déterminé et l'ensemble
déterminé et l'ensemble
![]() construit, il est possible d'augmenter le flot principal de l'arc pour atteindre
construit, il est possible d'augmenter le flot principal de l'arc pour atteindre
![]() , en utilisant les couples restants de l'ensemble
, en utilisant les couples restants de l'ensemble
![]() . La méthode complète détermine, pour chaque SP-relation, son flot
minimal à partir des deux sous-graphes déjà optimisés, cette
opération nécessite
. La méthode complète détermine, pour chaque SP-relation, son flot
minimal à partir des deux sous-graphes déjà optimisés, cette
opération nécessite
![]() opérations,
opérations,
![]() étant la cardinalité de l'ensemble
étant la cardinalité de l'ensemble
![]() . Comme pour l'agrégation,
. Comme pour l'agrégation,
![]() ne peut dépasser
ne peut dépasser
![]() , pour chaque SP-relation il faut donc
, pour chaque SP-relation il faut donc
![]() opérations. Le graphe contient
opérations. Le graphe contient
![]() SP-relations, cette méthode effectue donc
SP-relations, cette méthode effectue donc
![]() opérations.
opérations.
Cette complexité n'est pas la meilleure que l'on puisse obtenir pour le problème du flot compatible, mais la méthode est simple à implémenter. En outre les résultats numériques montrent que le temps passé dans cette phase de la méthode de reconstruction est négligeable, la méthode employée pour déterminer un flot compatible n'altère pas les performances globales de la méthode de reconstruction (e.g. tableau 5.6).
| 5.3.2.2. Complexité et résultats numériques |
Notons
![]() le nombre de composantes de la SP-décomposition du graphe
le nombre de composantes de la SP-décomposition du graphe
![]() utilisée pour la reconstruction. Pour chaque composante
utilisée pour la reconstruction. Pour chaque composante
![]() dont le nombre d'arcs est
dont le nombre d'arcs est
![]() , la méthode effectue une opération d'agrégation (soit
, la méthode effectue une opération d'agrégation (soit
![]() opérations), une opération de désagrégation (soit
opérations), une opération de désagrégation (soit
![]() opérations pour construire la tension et
opérations pour construire la tension et
![]() opérations pour construire le flot) et une opération de reconstruction,
i.e. la mise à conformité d'un arc (soit
opérations pour construire le flot) et une opération de reconstruction,
i.e. la mise à conformité d'un arc (soit
![]() opérations). Le nombre total d'opérations est
opérations). Le nombre total d'opérations est
![]() , or
, or
![]() , donc
, donc
![]() . La méthode complète, hors décomposition du graphe en
SP-composantes, nécessite alors
. La méthode complète, hors décomposition du graphe en
SP-composantes, nécessite alors
![]() opérations. Remarquons que si le graphe est décomposé en
opérations. Remarquons que si le graphe est décomposé en
![]() composantes, une par arc, on retrouve la complexité de la mise à
conformité.
composantes, une par arc, on retrouve la complexité de la mise à
conformité.
Nous proposons maintenant une comparaison sur le plan pratique de la méthode de reconstruction par rapport aux deux méthodes les plus efficaces sur des graphes quelconques: la mise à l'échelle du dual et la mise à conformité. Pour connaître en détails comment ont été dirigés ces essais (méthode de génération des problèmes, compilateur utilisé...), le lecteur peut consulter l'annexe. Nous précisons seulement ici que les problèmes générés ont des bornes de tension et des coûts entiers. Le nombre d'itérations pour la méthode de mise à conformité et la reconstruction est le nombre de recherches de cycle et de cocycle effectuées. Les temps de calcul sont exprimés en secondes sur une machine RISC-6000 à 160 MHz.
Les résultats présentés ici ne prennent pas en compte la phase de décomposition, puisque la SP-décomposition des graphes est déterminée au moment de leur génération. Il faut savoir que la décomposition n'est pas optimale dans le sens où elle ne contient pas forcément l'une des plus grandes SP-composantes maximales, mais elle en est très proche. En effet, les graphes sont générés à partir d'un graphe série-parallèle en lui ajoutant aléatoirement les arcs manquants pour obtenir la SP-perturbation souhaitée. Mais ces ajouts peuvent tout à fait rajouter des opérations parallèles dans le graphe, et agrandir la composante série-parallèle de départ.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Tableau 5.2: Résultats numériques de la méthode de
reconstruction sur des graphes presque série-parallèles, influence de la dimension du graphe. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Le tableau 5.2 montre le temps de résolution des algorithmes pour différentes
tailles de graphe (avec
![]() ) et une SP-perturbation fixe de
) et une SP-perturbation fixe de
![]() . La méthode de reconstruction se comporte mieux que les deux autres
méthodes, notamment en comparaison avec la méthode de mise à
conformité, puisqu'elle effectue beaucoup moins d'itérations. Cependant, comme elle
manipule des coûts linéaires avec plus de deux morceaux, chaque itération de la
mise à conformité est ralentie d'un facteur constant.
. La méthode de reconstruction se comporte mieux que les deux autres
méthodes, notamment en comparaison avec la méthode de mise à
conformité, puisqu'elle effectue beaucoup moins d'itérations. Cependant, comme elle
manipule des coûts linéaires avec plus de deux morceaux, chaque itération de la
mise à conformité est ralentie d'un facteur constant.
Le tableau 5.3 s'intéresse au comportement des méthodes en fonction de la
SP-perturbation du graphe (avec
![]() ,
,
![]() et
et
![]() ). La méthode de reconstruction reste la plus efficace jusqu'à
). La méthode de reconstruction reste la plus efficace jusqu'à
![]() de SP-perturbation, à partir de ce seuil la mise à l'échelle du
dual, la plus efficace sur des graphes quelconques, redevient compétitive. Notons la
stabilité de la mise à l'échelle qui, même si elle ne donne pas ses
meilleures performances ici, est totalement insensible à la SP-perturbation, ce qui veut
dire qu'avec
de SP-perturbation, à partir de ce seuil la mise à l'échelle du
dual, la plus efficace sur des graphes quelconques, redevient compétitive. Notons la
stabilité de la mise à l'échelle qui, même si elle ne donne pas ses
meilleures performances ici, est totalement insensible à la SP-perturbation, ce qui veut
dire qu'avec
![]() de perturbation les graphes possèdent toujours une structure
particulière qui handicape la méthode. A la vue des résultats
numériques, nous décidons qu'une SP-perturbation de
de perturbation les graphes possèdent toujours une structure
particulière qui handicape la méthode. A la vue des résultats
numériques, nous décidons qu'une SP-perturbation de
![]() est un seuil raisonnable pour déclarer un graphe presque
série-parallèle, c'est la valeur au delà de laquelle la mise à
conformité simple est plus efficace que la méthode de reconstruction.
est un seuil raisonnable pour déclarer un graphe presque
série-parallèle, c'est la valeur au delà de laquelle la mise à
conformité simple est plus efficace que la méthode de reconstruction.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Tableau 5.3: Résultats numériques de la méthode de
reconstruction sur des graphes presque série-parallèles, influence de la SP-perturbation du graphe. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 5.3.3. Méthodes de décomposition |
Dans les résultats numériques précédents, nous avons omis
volontairement la phase de décomposition d'un graphe en composantes
série-parallèles, afin de mettre en évidence le potentiel de la méthode
de reconstruction. Les tests ont été effectués sur des graphes dont une bonne
SP-décomposition était fournie (de la façon dont elle a été
obtenue, il est raisonnable de penser que la décomposition contient une SP-composante
très proche d'une des plus grandes composantes maximales), et ils montrent que la
méthode de reconstruction est potentiellement efficace pour des graphes avec une
SP-perturbation inférieure à
![]() .
.
Il est donc nécessaire maintenant de proposer une méthode qui, pour un graphe quelconque, propose une SP-décomposition avec l'une des plus grandes composantes maximales. Le problème similaire pour les graphes planaires a été étudié et s'avère être NP-complet (cf. [Liu77]). La plupart des algorithmes à l'heure actuelle tentent de déterminer de bonnes solutions approchées. Les graphes série-parallèles sont planaires, mais il n'est pas sûr que le problème soit difficile pour cette classe de graphes.
A notre connaissance il n'existe pas de travaux pour déterminer une plus grande
composante maximale série-parallèle d'un graphe quelconque. Nous ne démontrons
pas ici la complexité du problème, ni même ne proposons une méthode
exacte. Dans notre cas, il ne faut pas consacrer trop de temps dans l'étape de
décomposition, l'efficacité de la phase de reconstruction pourrait alors être
perdue. Nous avons donc choisi d'élaborer deux méthodes rapides et simples à
implémenter, puisqu'elles reposent sur les deux algorithmes de reconnaissance de graphe
série-parallèle vus précédemment (cf. les algorithmes 5.1 et 5.4). Ces
méthodes n'offrent naturellement pas la meilleure SP-décomposition d'un graphe, mais
elles permettent tout de même à la méthode de reconstruction de rester efficace
jusqu'à
![]() de SP-perturbation.
de SP-perturbation.
Les deux approches reposent sur la même idée. Lors de la reconnaissance du graphe, c'est un blocage de la procédure qui permet de détecter que le graphe n'est pas série-parallèle. Dans la première méthode, il n'est plus possible de réduire le graphe. Dans la seconde méthode, il y a deux possibilités: soit les signatures de deux arcs entrants d'un noeud de synchronisation sont différentes, soit il y a un circuit dans le graphe et le parcours est stoppé. Dans ces trois cas, il est possible, en supprimant judicieusement un ou plusieurs arcs de continuer la reconnaissance, le graphe n'est bien entendu pas série-parallèle, mais l'identification de la structure série-parallèle continue. Les arcs ainsi enlevés représentent chacun une SP-composante. Si l'arc est agrégé, la composante est un sous-graphe, sinon il s'agit d'un simple arc.
Il faut noter également que l'ordre imposé à la SP-décomposition, pour que la procédure de reconstruction fonctionne, est facile à obtenir avec cette approche. Les arcs sont retirés du graphe dans un certain ordre, en inversant cet ordre, la SP-décomposition est triée comme souhaité. En effet, au moment où l'on retire un arc, ses extrémités sont encore dans le graphe, la ou les composantes les contenant seront retirées par la suite, et se trouveront alors avant l'arc dans la SP-décomposition. Penchons-nous maintenant, pour les deux approches de reconnaissance, sur les stratégies intuitives élaborées pour sélectionner le ou les arcs à retirer au moment du blocage de la procédure.
| 5.3.3.1. Approche par réduction |
Pour reconnaître un graphe série-parallèle, cette méthode
réduit successivement les relations séries et parallèles simples du graphe.
Lorsque la procédure s'arrête, soit il reste un seul arc dans le graphe et à ce
moment le graphe est série-parallèle, soit il faut décider d'enlever un arc
pour poursuivre les réductions. En supprimant un arc, il est impossible de faire
apparaître une relation parallèle, en revanche des relations séries (au maximum
![]() ) peuvent être révélées. Une manière intuitive de
procéder consiste, en cas de blocage, à supprimer l'arc qui fait apparaître le
plus de relations séries, et s'il n'en existe aucun, il faut alors sélectionner celui
qui en favorisera le plus. Pour cela, nous avons choisi d'attribuer à chaque noeud
) peuvent être révélées. Une manière intuitive de
procéder consiste, en cas de blocage, à supprimer l'arc qui fait apparaître le
plus de relations séries, et s'il n'en existe aucun, il faut alors sélectionner celui
qui en favorisera le plus. Pour cela, nous avons choisi d'attribuer à chaque noeud
![]() deux scores, l'un qui sera utilisé lorsque
deux scores, l'un qui sera utilisé lorsque
![]() est l'origine d'un arc (i.e. le score
est l'origine d'un arc (i.e. le score
![]() ), et l'autre lorsqu'il est la destination d'un arc (i.e. le score
), et l'autre lorsqu'il est la destination d'un arc (i.e. le score
![]() ). Le score d'un arc
). Le score d'un arc
![]() est la somme
est la somme
![]() , les scores des noeuds étant calculés de la manière suivante.
, les scores des noeuds étant calculés de la manière suivante.
Intuitivement, le noeud
![]() avec
avec
![]() et
et
![]() est le meilleur candidat pour être l'origine de l'arc à supprimer, il
fait apparaître une relation série et totalise un score de
est le meilleur candidat pour être l'origine de l'arc à supprimer, il
fait apparaître une relation série et totalise un score de
![]() . De la même manière, le noeud
. De la même manière, le noeud
![]() avec
avec
![]() et
et
![]() est le meilleur candidat pour être la destination de l'arc à supprimer.
Un arc qui fait apparaître deux relations séries totalise donc un score de
est le meilleur candidat pour être la destination de l'arc à supprimer.
Un arc qui fait apparaître deux relations séries totalise donc un score de
![]() . Ce score décroît ensuite plus les extrémités de l'arc
possèdent des degrés entrant et sortant élevés, puisque cela signifie
de nombreuses suppressions d'arc avant qu'elles soient une relation série. Les suppressions
d'arc altérant la connexité du graphe sont pénalisées d'un score
négatif, ainsi un noeud qui risque d'obtenir un degré entrant ou sortant nul se voit
attribué un score de
. Ce score décroît ensuite plus les extrémités de l'arc
possèdent des degrés entrant et sortant élevés, puisque cela signifie
de nombreuses suppressions d'arc avant qu'elles soient une relation série. Les suppressions
d'arc altérant la connexité du graphe sont pénalisées d'un score
négatif, ainsi un noeud qui risque d'obtenir un degré entrant ou sortant nul se voit
attribué un score de
![]() ,
,
![]() doit être choisi de manière à ce que même le meilleur score
de la seconde extrémité de l'arc ne puisse pas remonter le score de l'arc au dessus
de 0, toute valeur
doit être choisi de manière à ce que même le meilleur score
de la seconde extrémité de l'arc ne puisse pas remonter le score de l'arc au dessus
de 0, toute valeur
![]() peut donc convenir. La figure 5.20 montre un exemple de scores. Les arcs
peut donc convenir. La figure 5.20 montre un exemple de scores. Les arcs
![]() et
et
![]() totalisent le meilleur score, et supprimer l'un ou l'autre permet bien de poursuivre
la réduction du graphe par deux relations séries et une relation parallèle.
totalisent le meilleur score, et supprimer l'un ou l'autre permet bien de poursuivre
la réduction du graphe par deux relations séries et une relation parallèle.
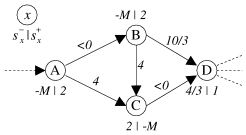 |
| Figure 5.20: Un exemple de score pour une SP-décomposition. |
En cas d'égalité de scores, c'est l'arc qui représente le plus petit
sous-graphe série-parallèle qui est éliminé, ainsi un arc
agrégé sera toujours préservé face à un arc non
agrégé, et l'on espère dégager de cette manière une plus grande
composante série-parallèle au final. L'algorithme de décomposition ainsi
formé a une complexité identique à celle de l'algorithme de reconnaissance par
réduction sur lequel il repose (i.e.
![]() opérations), car la sélection d'un arc à éliminer
nécessite
opérations), car la sélection d'un arc à éliminer
nécessite
![]() opérations (pour attribuer un score à tous les arcs du graphe).
opérations (pour attribuer un score à tous les arcs du graphe).
| 5.3.3.2. Approche par chemin |
Dans cette approche, l'identification d'un graphe non série-parallèle survient de
deux manières. La première se produit lors du parcours des noeuds dans un ordre
topologique, s'il existe un circuit dans le graphe, il arrive un moment où le parcours ne
peut plus continuer, et le circuit passe forcément par l'un des noeuds visités en
dernier (i.e. noeuds pour lesquels leurs prédécesseurs et eux mêmes ont
été visités, mais pas tous leurs successeurs), notons
![]() l'ensemble de ces noeuds. En effet, plus aucun noeud ne peut être visité
car dans l'ensemble
l'ensemble de ces noeuds. En effet, plus aucun noeud ne peut être visité
car dans l'ensemble
![]() , deux noeuds au moins sont mutuellement prédécesseurs l'un de l'autre,
directement ou indirectement. La procédure consiste alors pour chaque noeud de
, deux noeuds au moins sont mutuellement prédécesseurs l'un de l'autre,
directement ou indirectement. La procédure consiste alors pour chaque noeud de
![]() à vérifier que l'un de ses arcs entrants ne fait pas partie d'un
circuit. Une fois un tel circuit trouvé, l'arc entrant impliqué est
éliminé du graphe, et la procédure de reconnaissance peut reprendre.
L'algorithme 5.14 précise ce processus d'élimination.
à vérifier que l'un de ses arcs entrants ne fait pas partie d'un
circuit. Une fois un tel circuit trouvé, l'arc entrant impliqué est
éliminé du graphe, et la procédure de reconnaissance peut reprendre.
L'algorithme 5.14 précise ce processus d'élimination.
Algorithme 5.14: briserCircuit(graphe
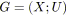 ,ensemble
,ensemble
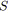 ,arc
,arc
 )
)


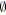 ; /* L'arc à éliminer. */
; /* L'arc à éliminer. */
tant que
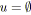 et
et
 faire
faire
soit
 un noeud de
un noeud de
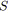 ;
;
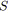

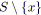 ;
;
pour tout
 et tant que
et tant que
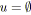 faire
faire
si
 alors
alors


 ;
;
sinon
/* On utilise l'algorithme de Minty avec la bonne
coloration */
/* (cf. section 2.1.4) pour rechercher le cycle. */
cycleMinty( ,
,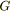 ,
,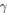 ,
, );
);
si
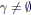 alors
alors


 ;
;
fin si;
fin pour;
fin tant que;
fin algorithme; La seconde manière d'identifier un graphe non-série parallèle survient
lorsqu'à la visite d'un noeud
![]() , il est impossible d'établir une synchronisation, i.e. un arc entrant
, il est impossible d'établir une synchronisation, i.e. un arc entrant
![]() possède une signature différente de tous les autres arcs entrants de
possède une signature différente de tous les autres arcs entrants de
![]() .
.
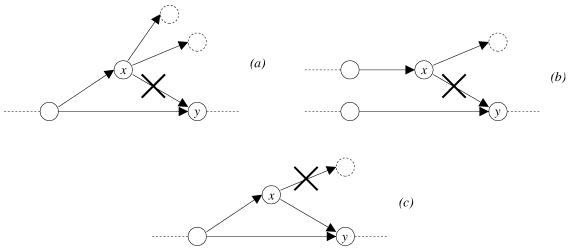 |
| Figure 5.21: Des exemples de situations de suppression d'arc. |
Deux possibilités intuitives s'offrent alors, supprimer cet arc (cf. figure 5.21a) ou
bien s'il est issu d'un noeud de branchement
![]() de degré sortant
de degré sortant
![]() , vérifier que la suppression de son voisin (i.e. le second arc sortant de
, vérifier que la suppression de son voisin (i.e. le second arc sortant de
![]() ) ne lui permet pas d'obtenir une signature identique à l'un des arcs entrants de
) ne lui permet pas d'obtenir une signature identique à l'un des arcs entrants de
![]() (cf. figures 5.21b et 5.21c). Pour cela, il suffit de vérifier que la signature
de l'arc entrant de
(cf. figures 5.21b et 5.21c). Pour cela, il suffit de vérifier que la signature
de l'arc entrant de
![]() , s'il existe, possède une signature identique à celle de l'un des arcs
entrants de
, s'il existe, possède une signature identique à celle de l'un des arcs
entrants de
![]() . En résumé, quand un arc
. En résumé, quand un arc
![]() bloque la procédure de reconnaissance, soit on le supprime, soit on supprime
son voisin au branchement
bloque la procédure de reconnaissance, soit on le supprime, soit on supprime
son voisin au branchement
![]() si cela permet ensuite la synchronisation de l'arc
si cela permet ensuite la synchronisation de l'arc
![]() avec l'un de ses voisins entrants de
avec l'un de ses voisins entrants de
![]() . L'algorithme 5.15 détaille cette procédure d'élimination.
. L'algorithme 5.15 détaille cette procédure d'élimination.
Algorithme 5.15: supprimerArc(graphe
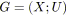 ,arc
,arc
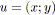 )
)
si
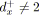 ou
ou
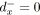 alors /* Supprimer
alors /* Supprimer
 . */
. */
sinon
soit
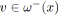 ;
;
si
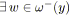 tel que
tel que
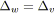 alors /* Supprimer
alors /* Supprimer
 . */
. */
sinon
soit
 tel que
tel que
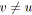 ;
;
/* Supprimer
 . */
. */
fin si;
fin si;
fin algorithme; L'algorithme de décomposition résultant a une complexité identique
à celle de l'algorithme de reconnaissance par chemin sur lequel il repose (i.e.
![]() opérations), car la sélection d'un arc à éliminer
nécessite
opérations), car la sélection d'un arc à éliminer
nécessite
![]() opérations (pour vérifier les signatures des arcs entrants du noeud
considéré).
opérations (pour vérifier les signatures des arcs entrants du noeud
considéré).
| 5.3.3.3. Résultats numériques |
Les résultats numériques présentés ici comparent les deux approches de décomposition en termes de rapidité d'exécution et également de qualité de la décomposition. Pour évaluer le deuxième critère, la SP-décomposition obtenue au moment de la génération aléatoire des instances sera utilisée comme référence. Même si elle n'est pas optimale dans le sens où elle ne contient pas forcément la plus grande SP-composante du graphe, elle en est certainement très proche, et nous permet donc de juger tout de même de la qualité des décompositions proposées par les deux approches.
Le tableau 5.4 montre le temps de calcul de chaque méthode avec le nombre de composantes
qu'elle a obtenue pour différentes tailles de graphe (avec une SP-perturbation fixée
à
![]() ). Le tableau 5.5 met en évidence le comportement des méthodes en
fonction de la SP-perturbation du graphe (avec
). Le tableau 5.5 met en évidence le comportement des méthodes en
fonction de la SP-perturbation du graphe (avec
![]() et
et
![]() ).
).
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Tableau 5.4: Comparaison des méthodes de SP-décomposition, influence de la dimension du graphe. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Pour une SP-perturbation de quelques pourcents, les deux méthodes semblent finalement très proches. L'approche par réduction propose néanmoins des décompositions apparemment de meilleure qualité, puisqu'elles possèdent moins de composantes. En revanche, elle est un peu moins rapide que l'approche par chemin pour une SP-perturbation raisonnable, et devient inefficace pour une forte SP-perturbation. Les résultats numériques présentés en conclusion montreront que la vitesse de décomposition obtenue par nos approches n'est pas un facteur décisif pour choisir entre les deux méthodes, en raison du faible degré de SP-perturbation. Le temps de décomposition est négligeable par rapport au temps de reconstruction. En revanche la qualité de la décomposition est beaucoup plus importante, car elle semble influer directement sur la vitesse de la phase de reconstruction.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Tableau 5.5: Comparaison des méthodes de SP-décomposition, influence de la SP-perturbation du graphe. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 5.3.4. Conclusion |
Pour conclure, nous présentons le comportement en pratique de la méthode de reconstruction complète, avec les deux méthodes de décomposition utilisant l'approche par réduction (A) et l'approche par chemin (B). En outre, les résultats détaillent le temps passé dans les principales étapes de la reconstruction: la décomposition (I), l'agrégation (II), la désagrégation (III) et la mise à conformité (IV).
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Tableau 5.6: Résultats numériques des méthodes de
reconstruction sur des graphes presque série-parallèles, influence de la dimension du graphe. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Le temps total de la méthode de reconstruction est indiqué dans la colonne (V). Pour connaître en détails comment ont été dirigés ces essais (méthode de génération des problèmes, compilateur utilisé...), le lecteur peut consulter l'annexe. Nous précisons seulement ici que les problèmes générés ont des bornes de tension et des coûts entiers. Le nombre d'itérations présenté correspond au nombre de recherches de cycle et de cocycle lors de la phase de mise à conformité. Les temps de calcul sont exprimés en secondes sur une machine RISC-6000 à 160 MHz.
Le tableau 5.6 montre le comportement des deux versions de la méthode de reconstruction
en fonction de la taille du graphe (avec une SP-perturbation de
![]() ), et le tableau 5.7 montre l'évolution de leurs performances par rapport
à la SP-perturbation (avec
), et le tableau 5.7 montre l'évolution de leurs performances par rapport
à la SP-perturbation (avec
![]() et
et
![]() ). On constate que le temps passé dans les phases d'agrégation et de
désagrégation est négligeable. Le temps d'exécution de la phase de
décomposition l'est un peu moins mais reste faible par rapport à celui de la phase de
mise à conformité. Comme nous l'avions déjà remarqué, la phase
de mise à conformité dans la reconstruction effectue peu d'itérations par
rapport à la méthode de mise à conformité seule, mais les
itérations sont plus longues à cause d'une structure de données plus lourde
pour manipuler des coûts linéaires avec plus de deux morceaux. Nous constatons aussi
que, moins il y a de SP-composantes, plus la reconstruction est rapide, l'approche par
réduction pour la décomposition semble mieux adaptée, mais elle ne rend la
reconstruction efficace que jusqu'à
). On constate que le temps passé dans les phases d'agrégation et de
désagrégation est négligeable. Le temps d'exécution de la phase de
décomposition l'est un peu moins mais reste faible par rapport à celui de la phase de
mise à conformité. Comme nous l'avions déjà remarqué, la phase
de mise à conformité dans la reconstruction effectue peu d'itérations par
rapport à la méthode de mise à conformité seule, mais les
itérations sont plus longues à cause d'une structure de données plus lourde
pour manipuler des coûts linéaires avec plus de deux morceaux. Nous constatons aussi
que, moins il y a de SP-composantes, plus la reconstruction est rapide, l'approche par
réduction pour la décomposition semble mieux adaptée, mais elle ne rend la
reconstruction efficace que jusqu'à
![]() de SP-perturbation.
de SP-perturbation.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Tableau 5.7: Résultats numériques des méthodes de
reconstruction sur des graphes presque série-parallèles, influence de la SP-perturbation du graphe. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Il ressort de ces résultats numériques deux points importants. Le premier est que la qualité de la SP-décomposition est importante pour l'efficacité de la phase de reconstruction. En outre, compte tenu du peu de temps consacré à la décomposition, il semble possible d'investir dans une méthode plus coûteuse mais donnant des SP-décompositions de meilleure qualité. Le second point est qu'il y a un réel décalage entre les performances de la mise à conformité pour des coûts linéaires avec deux morceaux et des coûts avec plus de morceaux. Un gain important de vitesse pourrait profiter à la méthode de reconstruction, en utilisant une structure de données plus performante pour représenter des coûts linéaires avec plus de deux morceaux.
| CONCLUSION |
Dans ce chapitre, une méthode d'agrégation tout à fait efficace, en
![]() opérations, a été proposée pour résoudre le
problème de la tension de coût minimal dans des graphes
série-parallèles. Cette classe d'instances étant trop idéale, il nous a
semblé important de considérer des graphes avec une structure plus réaliste.
Pour cela, nous proposons la notion peu formelle de graphe presque série-parallèle
qui permet toutefois d'appréhender et de mesurer la complexité de la structure d'un
graphe par rapport au problème de la tension de coût minimal.
opérations, a été proposée pour résoudre le
problème de la tension de coût minimal dans des graphes
série-parallèles. Cette classe d'instances étant trop idéale, il nous a
semblé important de considérer des graphes avec une structure plus réaliste.
Pour cela, nous proposons la notion peu formelle de graphe presque série-parallèle
qui permet toutefois d'appréhender et de mesurer la complexité de la structure d'un
graphe par rapport au problème de la tension de coût minimal.
Une méthode de reconstruction a été proposée pour ces graphes presque série-parallèles. Des résultats numériques, il ressort un potentiel intéressant de la méthode dont nous n'avons pas complètement réussi à profiter. Il faudrait en effet étudier des méthodes de décomposition d'un graphe quelconque en composantes série-parallèles, en expérimentant deux types d'optimalité: minimiser le nombre de composantes ou obtenir la composante maximale la plus grande.
Néanmoins, avec la méthode d'agrégation, la méthode de
reconstruction et les méthodes du chapitre précédent, il est possible de
proposer différents algorithmes pour le problème de la tension de coût minimal,
chacun étant efficace sur différentes structures de graphe: la mise à
l'échelle est très efficace sur des graphes a priori quelconques, la mise à
conformité prend le relais pour des graphes plus structurés, se rapprochant des
graphes presque série-parallèles et enfin l'agrégation s'avèrent
très efficace pour des graphes série-parallèles. La combinaison de la mise
à conformité et de l'agrégation permet de traiter plus efficacement le
problème de la tension de coût minimal sur des graphes presque
série-parallèles, que nous avons définis comme étant des graphes avec
une SP-perturbation inférieure à
![]() .
.
|